Revista IECOS, 25(2), 11-34 | Julio-Diciembre 2024 | ISSN 2961-2845 | e-ISSN 2788-7480
ANÁLISIS PROBABILÍSTICO DE LA PROGRAMACIÓN DE PROYECTOS, CÓMO INCORPORAR INCERTIDUMBRE EN LA GESTIÓN DE PROYECTOS
PROBABILISTIC ANALYSIS OF PROJECT SCHEDULING, HOW TO INCORPORATE UNCERTAINTY INTO PROJECT MANAGEMENT
José Salinas Ortiz![]()
Universidad Nacional de Ingeniería, Lima, Perú
E-mail: josesalinas@uni.edu.pe
https://orcid.org/0009-0000-3745-6392
https://doi.org/10.21754/iecos.v25i2.2235
Recibido (Received): 21/06/2024 Aceptado (Accepted): 10/07/2024 Publicado (Published): 27/09/2024
RESUMEN
La evaluación de proyectos debe considerar tanto los costos de inversión como los tiempos de culminación, ambos sujetos a incertidumbre. Este artículo presenta un enfoque para incorporar explícitamente la incertidumbre en los tiempos de duración de las actividades necesarias para completar un proyecto[1]. Los métodos PERT y CPM, ampliamente adoptados en la industria y el gobierno desde los años cincuenta, ayudan a gestionar la interdependencia de las actividades del proyecto. Aunque originalmente diferenciados en el manejo del tiempo y costo, estos métodos comparten la limitación de no considerar adecuadamente la incertidumbre. Se utilizan tres estimaciones de tiempo (optimista, más probable y pesimista) para un “análisis probabilístico” de la ruta crítica, pero este enfoque no aborda múltiples escenarios ni ajusta la ruta crítica en función de la variación real en los tiempos. Para superar estas limitaciones, se desarrolló un modelo en Excel que permite un análisis probabilístico más adecuado del tiempo de terminación del proyecto. El artículo detalla los objetivos del nuevo procedimiento y los pasos necesarios para incorporar la incertidumbre, utilizando un ejemplo simple de construcción de una planta industrial. Las conclusiones y recomendaciones se presentan al final del artículo.
Palabras claves: incertidumbre, proyecto, inversión, probabilístico, gestión.
ABSTRACT
Project evaluation must consider both investment costs and completion times, both of which are subject to uncertainty. This article presents an approach to explicitly incorporate the uncertainty in the duration of activities necessary to complete a project. The PERT and CPM methods, widely adopted in industry and government since the 1950s, help manage the interdependence of project activities. Although originally differentiated by their handling of time and cost, these methods share the limitation of not adequately considering uncertainty. They use three-time estimates (optimistic, most likely, and pessimistic) for a "probabilistic analysis" of the critical path, but this approach does not address multiple scenarios nor adjust the critical path based on actual time variations. To overcome these limitations, an Excel model was developed that allows for a more appropriate probabilistic analysis of the project's completion time. The article details the objectives of the new procedure and the steps necessary to incorporate uncertainty, using a simple example of constructing an industrial plant. Conclusions and recommendations are presented at the end of the article.
Keywords: uncertainty, project, investment, probabilistic, management.
1. INTRODUCCIÓN
Los proyectos de inversión pueden variar significativamente en complejidad y tiempo de implementación, lo que hace que completar los proyectos a tiempo sea una tarea desafiante. Las complicaciones surgen al programar estos proyectos, que a menudo se estructuran mediante la interdependencia de las actividades necesarias para su culminación. Generalmente, ciertas actividades no pueden comenzar antes de que otras hayan terminado. En grandes proyectos, pueden existir numerosas relaciones de dependencia, lo que requiere métodos efectivos de análisis.
Los métodos PERT (Program Evaluation Review Technique) y CPM (Critical Path Method) fueron desarrollados a finales de los años cincuenta y recibieron una gran publicidad, lo que facilitó su aceptación en diversas ramas de la industria y el gobierno (Anderson et al. 2015). Estos métodos se han aplicado en proyectos tan diversos como la construcción de fábricas, carreteras, desarrollo de nuevos productos, y diseño e instalación de nuevos sistemas. Actualmente, muchas empresas y agencias gubernamentales y multinacionales exigen que todos sus contratistas utilicen estos métodos.
Inicialmente, las diferencias entre PERT y CPM se centraban en cómo se manejaban el tiempo y el costo. Sin embargo, en la práctica, estas diferencias se han ido diluyendo a medida que las empresas han integrado las mejores características de ambos métodos para gestionar sus proyectos de manera más eficiente (Munier, 1981). No obstante, un aspecto que no se ha considerado adecuadamente es la incertidumbre tanto en los costos como en los tiempos de las actividades del proyecto.
Se reconoce que los tiempos de las actividades a menudo no se conocen con certeza, y se incorpora la incertidumbre utilizando tres estimaciones: optimista (o), como tiempo mínimo; más probable (m), como tiempo normal; y pesimista (p), como tiempo máximo. Luego, se asume que la duración de la actividad sigue una distribución de probabilidades unimodal beta, lo que permite estimar el valor esperado del tiempo de la actividad [(o + 4m + p)/6]. Con estos estimados, muchos programas de computación (por ejemplo, Microsoft Project) realizan un análisis "probabilístico" de la ruta crítica definiendo tres escenarios:
· Escenario optimista, cuando todos los tiempos de las actividades toman su valor optimista.
· Escenario pesimista, cuando todos los tiempos de las actividades toman su valor pesimista.
· Escenario medio, cuando todos los tiempos de las actividades toman su valor esperado.
La limitación de este enfoque es que no considera la multiplicidad de escenarios (por ejemplo, si existen cinco actividades críticas, se tendrán 35 = 243 escenarios utilizando tres valores por cada actividad) ni calcula la probabilidad asociada a cada escenario. Además, no se toma en cuenta que, si una actividad crítica se termina suficientemente temprano, la ruta crítica puede cambiar; o que, si una actividad no crítica se retrasa lo suficiente, puede convertirse en parte de una nueva ruta crítica.
Estas limitaciones nos llevaron a crear un modelo bien estructurado en Excel, que permite realizar un análisis realmente probabilístico del tiempo de terminación de los proyectos utilizando software especializado.
En la sección 2 se plantea los objetivos del procedimiento propuesto y en la sección 3 se detalla los pasos necesarios para incorporar la incertidumbre y hacer un análisis probabilístico del tiempo de culminación del proyecto. Dada la naturaleza tutorial de este artículo se usa un ejemplo simple de un proyecto para la construcción de una planta industrial. En la sección 4 se plantean las conclusiones y recomendaciones.
2. OBJETIVO
El presente procedimiento tiene por objetivo establecer pautas para:
· Incorporar la incertidumbre en el análisis del tiempo de terminación del proyecto.
· Utilizar el conocimiento de los expertos del proyecto (personas que conocen bien las actividades que conforman el proyecto) para valorar el nivel de incertidumbre en la duración de las actividades.
· Responder preguntas como:
o ¿Cuál es la fecha esperada de término del proyecto?
o ¿Cuál es el rango de incertidumbre en la fecha de término del proyecto?
o ¿Cuál es el perfil del tiempo de terminación del proyecto?
o ¿Cuál es la probabilidad de terminar el proyecto antes de una fecha preestablecida?
El procedimiento planteado permite contestar estas preguntas y muchas más, proporcionando un análisis detallado y probabilístico del tiempo de terminación del proyecto. Este procedimiento se basaen los entendimientos de la Disciplina del Analisis de Decisiones (Howard, 1966; Salinas, 2009) y de una aplicación concreta (Salinas 2004).
3. PROCESO PARA ESTIMAR EL TIEMPO DE PUESTA EN OPERACIÓN DE LOS PROYECTOS
Para responder las preguntas planteadas, utilizaremos un proceso de ocho pasos[2]:
1º. Definir la red PERT: Identificar las actividades necesarias para completar el proyecto y describir sus relaciones en términos de predecesores inmediatos.
2º. Obtener los rangos de incertidumbre en la duración de las actividades: Entrevistar a los expertos para obtener una primera aproximación del grado de incertidumbre en los tiempos de duración de las actividades.
3º. Crear el modelo en hoja de cálculo: Estructurar la red PERT en una hoja de cálculo con secciones claramente definidas para introducir las actividades del proyecto y sus rangos de incertidumbre. Describir las relaciones de precedencia para calcular el tiempo de terminación del proyecto.
4º. Hacer el análisis de sensibilidad: Utilizar Sensitivity®, un software especializado, para identificar las actividades críticas que generan incertidumbre en el tiempo de culminación del proyecto (Supertree Software, s.f.).
5º. Construir el modelo probabilístico: Con los tiempos de las actividades críticas identificadas, construir un árbol de probabilidades que describa los posibles escenarios y sus probabilidades de ocurrencia.
6º. Establecer la distribución de probabilidades del tiempo de culminación del proyecto: Utilizar Supertree®, un software especializado, para establecer el perfil (distribución de probabilidades) de duración del proyecto (Supertree Software, s.f.).
7º. Análisis probabilístico: Analizar el perfil de duración del proyecto para determinar la probabilidad de que el proyecto termine antes de un periodo preestablecido, y calcular la duración esperada o promedio de terminación del proyecto.
8º. Resumen y conclusiones. El perfil del proyecto y el análisis probabilístico permitirán responder las preguntas planteadas anteriormente y muchas más.
A continuación, se presenta el proceso, sus pasos y técnicas esenciales, con un ejemplo simple de un proyecto para la construcción de una planta industrial. El contrato incluye una multa significativa si no se termina la construcción en 43 semanas, por lo que un elemento clave es evaluar la probabilidad de completar el proyecto antes de ese plazo.
3.1. Primer paso: Definir la red PERT
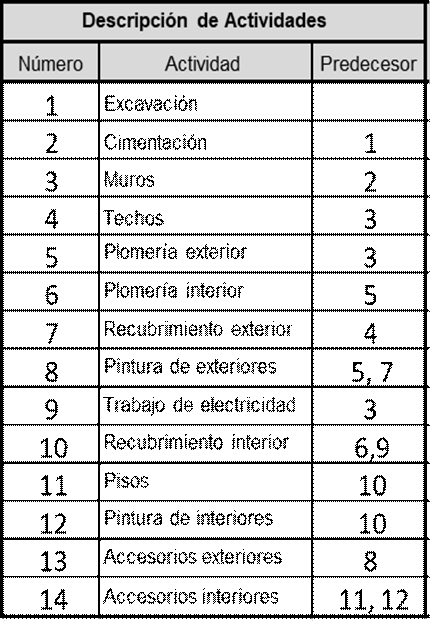
En este paso, se identifican las actividades específicas que conforman el proyecto en análisis. Esto implica elaborar una lista de todas las actividades necesarias para completar el proyecto, junto con sus predecesores inmediatos. Estos predecesores describen la interdependencia entre las actividades, indicando que algunas deben completarse antes de que otras puedan comenzar. Esta tarea se facilitará mediante la información proporcionada por los expertos en el proyecto. En el proyecto demostrativo, hay 14 actividades principales para llevar a cabo esta construcción; la lista de actividades con sus predecesores inmediatos se muestra en la Tabla 1.
En este ejemplo, sólo tres actividades tienen más de un predecesor inmediato: las actividades 8, 10 y 14. La actividad 8 (pintura de exteriores) tiene como predecesores inmediatos las actividades 5 y 7. Esto significa que la plomería exterior (actividad 5) y el recubrimiento exterior (actividad 7) deben completarse antes de que pueda comenzar la pintura de exteriores.
Tabla 1
Listado de actividades con sus predecesores
Con base en este listado, se puede dibujar una figura que no solo represente las actividades enumeradas, sino también las relaciones de predecesores entre ellas. Esta representación, conocida como la red PERT del proyecto, permite visualizar gráficamente el orden en que se llevarán a cabo las actividades (Anderson et al., 2015).
Figura 1
Red Pert del proyecto demostrativo
 |
3.2. Segundo paso: Obtener los rangos de incertidumbre en la duración de las actividades del proyecto.
Una vez establecida la red PERT del proyecto, se necesita información sobre el tiempo requerido para terminar cada actividad. Esta información se utilizará para calcular la duración total del proyecto.
Lamentablemente, los estimados del tiempo de duración de cada actividad pueden ser difíciles de obtener. En muchos casos, la duración de cada actividad es incierta y puede describirse inicialmente mediante un rango de valores posibles que reflejan el grado de incertidumbre percibido por los expertos.
Para incorporar tiempos inciertos en el análisis, se necesita una primera aproximación del grado de incertidumbre específico a los tiempos de las actividades individuales (Salinas, 2009). A partir de entrevistas con expertos, se determinan los rangos de incertidumbre para la duración de las actividades del proyecto, definiendo tres valores:
· Valor bajo: Representa el primer decil; es decir, hay un 10% de probabilidad de que el tiempo de duración de la actividad sea menor o igual a este valor.
· Valor medio: Representa el quinto decil (o mediana); es decir, hay un 50% de probabilidad de que el tiempo de duración de la actividad sea menor o igual a este valor.
· Valor alto: Representa el noveno decil; es decir, hay un 10% de probabilidad de que el tiempo de duración de la actividad sea mayor a este valor.
En el caso del proyecto demostrativo, los rangos de incertidumbre obtenidos de los expertos para la duración de cada una de las actividades identificadas se muestran en la Tabla 2.
Tabla 2
Listado de actividades con sus rangos de incertidumbre
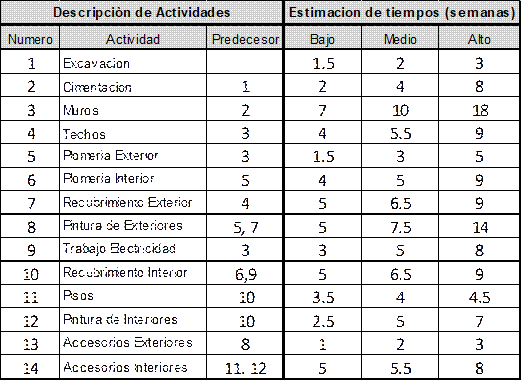
La Tabla 2 muestra que el grado de incertidumbre es específico a cada actividad. Por ejemplo, los expertos consideran que la incertidumbre en la duración del levantamiento de los muros oscila entre 7 y 18 semanas, con una probabilidad del 80%, y estiman que la duración promedio (mediana) es de 10 semanas. En contraste, la incertidumbre en la duración de la puesta de pisos es de solo una semana.
3.3. Tercer paso: Crear el modelo en hoja de cálculo.
En este paso, se construye un modelo en Excel, el cual debe estar bien organizado para facilitar el análisis probabilístico. Este modelo consta de tres secciones claramente definidas, como se muestra en la Figura 2 (Salinas, 2009).
La sección de inputs se localiza en la parte superior de la hoja de cálculo y contiene todos los parámetros de entrada del modelo: las constantes y los rangos de incertidumbre de la duración de las actividades (bajo, medio, alto).
Figura 2
Estructura del modelo en hoja de cálculo
 |
Se asignan nombres a las variables de entrada, es decir, a los tiempos de las actividades, que se usarán en los cálculos en lugar de referencias a celdas. Se pueden asignar múltiples nombres a la vez usando los comandos:
· Fórmulas/ Crear desde la selección/ Columna derecha
Siguiendo estas pautas, la sección de inputs queda determinada como se muestra en la Tabla 3.
Tabla 3
Sección de inputs del modelo en hoja de cálculo
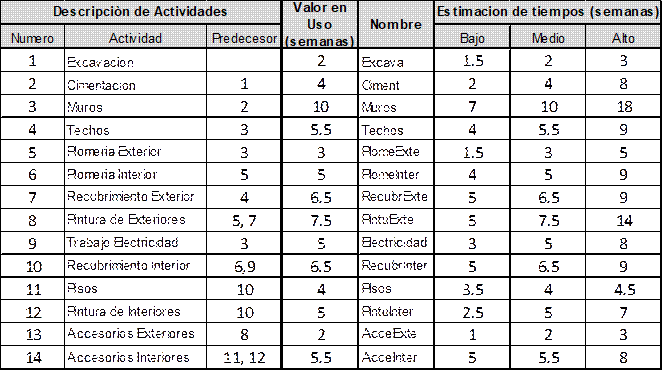
En esta sección, se puede incluir cualquier tipo de proyecto, desde proyectos simples con pocas actividades hasta proyectos complejos con muchas actividades, como los proyectos hidroeléctricos. La única restricción es contar con el acceso a expertos que puedan describir estos proyectos en términos de redes PERT y establecer los rangos de incertidumbre en los tiempos de sus actividades (Salinas, 2009).
En la sección de cálculos, se realizan todas las operaciones necesarias para determinar el tiempo de terminación del proyecto y otros valores relevantes. Los cálculos describen las relaciones entre las actividades establecidas en la sección de inputs, en términos de inicio, duración y culminación de cada actividad que forma el proyecto.
Recordemos que para iniciar una actividad específica deben culminarse las actividades que son sus predecesores inmediatos. Con este concepto, podemos calcular los tiempos de inicio (TIi) de cada actividad, su tiempo de duración (TDi) y, por lo tanto, su tiempo de término (TTi). Para las actividades sin predecesores, su tiempo de inicio será cero; para las otras actividades, sus tiempos de inicio estarán definidos por el mayor tiempo de término de sus predecesores inmediatos. Así tenemos, por ejemplo, para la actividad 4, que tiene como único predecesor a la actividad 3, las siguientes relaciones:
TI4 = TT3
TT4 = TI4 + TD4
En cambio, para la actividad 10, que tiene como predecesores a las actividades 6 y 9, las relaciones de sus tiempos de inicio y culminación se establecen de la siguiente manera:
TI10 = máximo (TT6, TT9)
TT10 = TI10 + TD10
Considerando estas relaciones, el área de cálculos queda definida de la siguiente manera:
Tabla 4
Sección de cálculos del modelo en hoja de cálculo
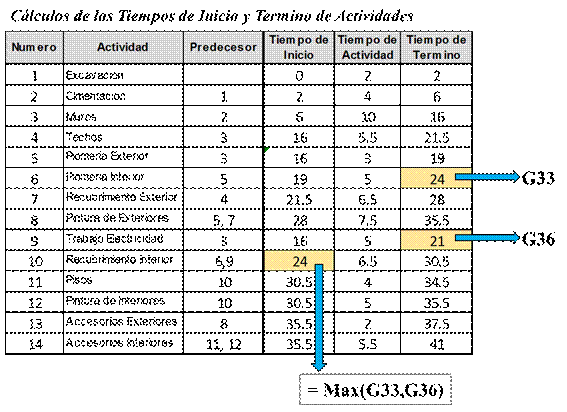
Es importante recordar que los tiempos de duración de las actividades considerados aquí son los tiempos medios, los cuales definen el caso o escenario base. Es decir, según los valores del caso base, cuando los tiempos de las actividades están fijados en su valor medio, el proyecto se culminará en 41 semanas. Sin embargo, este estimado no considera las incertidumbres. En el quinto paso de este proceso, se analizará la sensibilidad del tiempo de culminación del proyecto a variaciones en los inputs inciertos utilizando los rangos de incertidumbre de los tiempos de las actividades.
La sección de resumen muestra la información necesaria para evaluar la razonabilidad de los resultados del análisis. En este caso ilustrativo, la Figura 5 reporta el tiempo de terminación del proyecto y lo compara con un tiempo tope preestablecido.
Tabla 5
Sección de resumen del modelo en hoja de calculo

3.4. Cuarto paso: Análisis de sensibilidad determinístico.
En este paso, se medirá la sensibilidad del tiempo de terminación del proyecto (TTP) con respecto a los cambios en los tiempos de las actividades individuales del proyecto. Es decir, el análisis se centra en observar cómo estos cambios afectan el TTP, identificando así las incertidumbres clave en los tiempos de las actividades[3].
En el paso anterior, se evaluó el modelo con todos los tiempos del caso base (las medianas), obteniendo el escenario base del proyecto. Ahora, se realiza el análisis de sensibilidad con respecto a las incertidumbres en los tiempos de las actividades, representadas por los tres valores (bajo, medio y alto) estimados a partir de las entrevistas a los expertos en el proyecto (Salinas, 2009).
Partiendo nuevamente del caso base, con todos los tiempos fijados en su valor medio, el modelo se reevaluará cambiando uno por uno los valores bajos y altos de cada tiempo de duración de las actividades para generar los respectivos tiempos de terminación del proyecto (TTP). La diferencia entre los valores del TTP generados es una medida de cuán sensible es la terminación del proyecto a la incertidumbre en el tiempo de la actividad bajo análisis. Si los cambios en el tiempo de una actividad tienen un gran efecto en el TTP, su incertidumbre merece especial atención. Por otro lado, si el efecto no es significativo, la actividad se fija en su tiempo medio, convirtiéndose en una variable parametrizada.
Todas las incertidumbres que tengan el mayor efecto en el TTP son las incertidumbres cruciales que serán tratadas como tales en el análisis probabilístico del siguiente paso, mientras que las demás se fijarán en su valor medio.
Este análisis de sensibilidad se puede realizar eficientemente utilizando software especializado que realice los cambios de los valores del caso base y calcule el TTP para cada cambio. El software recomendado por su potencia y eficiencia para este análisis y el análisis probabilístico es Supertree®. La parte que realiza el análisis de sensibilidad determinístico se llama Sensitivity®, y es el utilizado en este proceso.
El uso de Sensitivity es muy sencillo: los datos de la sección de inputs del modelo en hoja de cálculo se importan de forma casi directa. Luego, Sensitivity usa el modelo en hoja de cálculo como su calculadora para calcular los diferentes valores del TTP asociados a cada valor de los tiempos de las actividades del proyecto. Finalmente, los resultados del análisis se representan gráficamente (diagrama de tornado) y en forma de tabla, permitiendo identificar directamente las incertidumbres cruciales.
El análisis de sensibilidad para el proyecto demostrativo muestra que el tiempo de culminación del proyecto es muy sensible a la incertidumbre en los tiempos de las actividades de levantamiento de muros, cimentación, plomería interior, recubrimiento interior y plomería exterior, como lo ilustra el diagrama de tornado en la Figura 3.
Figura 3
Tornado del Proyecto Demostrativo
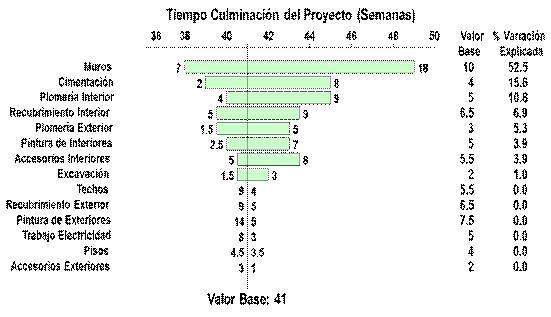
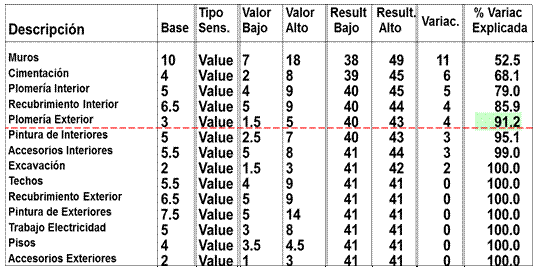
Esta misma información se presenta en forma de tabla, donde se observa que los tiempos de las dos actividades más críticas (muros y cimentación) explican el 68,1% de la variación total del TTP. Al añadir las incertidumbres en los tiempos de las actividades de plomería interior, recubrimiento interior y plomería exterior, se encuentra que estas cinco incertidumbres explican el 91,2% de la incertidumbre total en el TTP. Estas cinco variables serán consideradas en el análisis probabilístico del siguiente paso.
Tabla 6
Resultados del análisis de sensibilidad
3.5. Quinto paso: Construcción del modelo probabilístico
El objetivo principal de este paso es considerar explícitamente la incertidumbre en los tiempos de las actividades cruciales identificadas en el análisis de sensibilidad. Se usa el mismo modelo del paso anterior, pero en lugar de considerar un solo estimado determinístico para cada uno de los tiempos de las actividades cruciales, se incorporan distribuciones de probabilidades para estas incertidumbres. Esto permite establecer una distribución de probabilidades para el TTP, como se muestra esquemáticamente en la Figura 4.
Figura 4
Análisis determinístico vs análisis probabilístico

En este paso, lo primero es construir un árbol de decisiones genérico para mostrar la decisión de realizar o no el proyecto y los factores críticos en la generación de incertidumbre en el TTP. La Figura 5 muestra el árbol genérico para el proyecto demostrativo.
Figura 5
Árbol de probabilidades genérico

Luego, se deben asignar probabilidades a los tiempos de las actividades cruciales, utilizando el proceso de evaluación de variables inciertas mediante probabilidades[4]. Seguidamente, se construye el modelo probabilístico que relaciona las incertidumbres cruciales con la incertidumbre total en el TTP. La distribución de probabilidades resultante para el TTP se llama perfil del TTP, el cual se analizará en el siguiente paso.
Los valores asociados a cada incertidumbre y sus probabilidades respectivas se determinarán usando el proceso de evaluación de probabilidades. Con este proceso de cinco pasos, se obtendrá una distribución de probabilidades acumulada para cada tiempo de duración de las actividades cruciales. Estas distribuciones continuas se discretizarán mediante la fijación de tres rangos que no se superponen y cubren todos los posibles valores. Una buena aproximación consiste en establecer tres rangos con probabilidades de 0.25, 0.50 y 0.25 para los valores bajo, medio y alto, respectivamente. Estos valores se incorporan en el árbol de probabilidades, el cual definirá 243 escenarios (35 = 243: cinco incertidumbres con tres valores cada una).
Tomando como ejemplo la duración de la actividad de cimentación, usando la “rueda de probabilidades” en el proceso de cinco pasos, se obtiene un diagrama de dispersiones de las respuestas del experto, como el que se muestra en la Figura 6, al cual se ha "ajustado" una curva continua.
Figura 6
Curva de Distribución de Probabilidades Acumulada
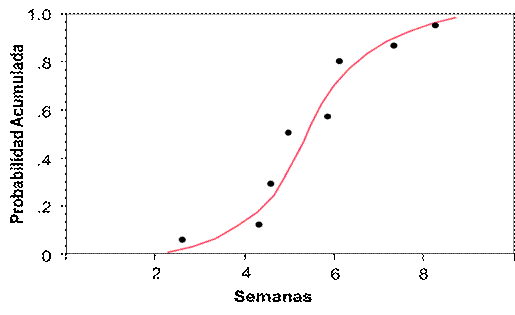
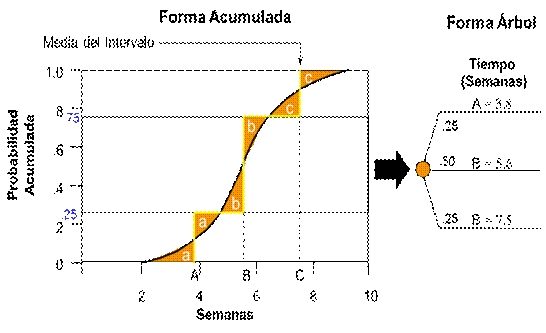
Luego, la distribución de probabilidades acumuladas continua se discretiza utilizando el criterio mencionado anteriormente, obteniendo una distribución discreta en forma de árbol, como se muestra en la Figura 7. Con estos nuevos valores, se alimenta el árbol de probabilidades en Supertree.
Figura 7
Representación de distribuciones continúas en una forma de árbol discreto
3.6. Sexto paso: Perfil del tiempo de culminación del proyecto
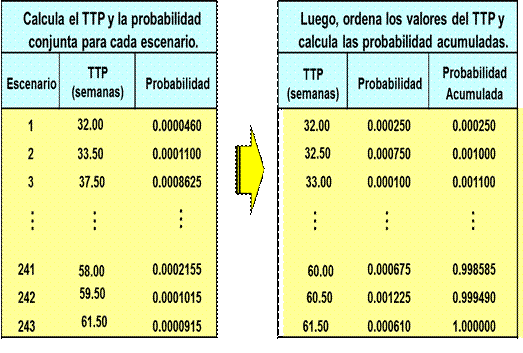
Con la ayuda de Supertree, se evalúa el árbol de probabilidades utilizando el modelo en hoja de cálculo. Esto permite calcular el TTP asociado a cada uno de los 243 escenarios definidos por las cinco incertidumbres críticas. Además, Supertree calcula la probabilidad asociada a cada escenario aplicando el concepto de expansión en cadena de la teoría de probabilidades (Salinas, 2009).
Posteriormente, Supertree facilita la construcción de la distribución de probabilidades acumulada de los diferentes valores del TTP asociados a los distintos escenarios (perfil de duración del proyecto). Esquemáticamente, se puede observar cómo Supertree ordena los TTP de menor a mayor y calcula las probabilidades acumuladas en la Figura 8.
Figura 8
Construcción de la distribución de probabilidades acumulada del TTP
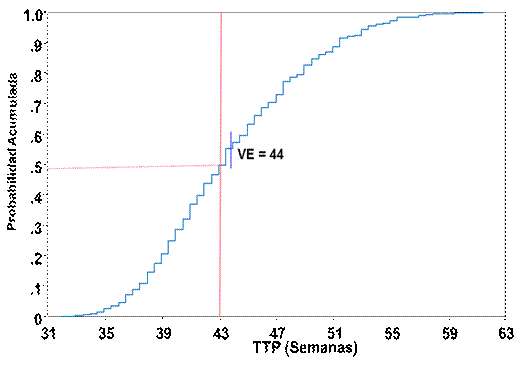
La distribución de probabilidad acumulada muestra el rango de los posibles valores del TTP y la probabilidad acumulada asociada a cada uno de ellos. La figura de estos valores y sus probabilidades acumuladas constituye el perfil del TTP, que se muestra en la figura 9. Este perfil del proyecto permite realizar el análisis probabilístico y responder a muchas preguntas de las partes interesadas del proyecto, tales como:
· ¿Cuál es el tiempo esperado de culminación del proyecto?
· ¿Cuál es la probabilidad de que el proyecto se termine antes de los 43 meses?
· ¿Debe incluirse este proyecto en el plan de obras para los próximos 43 meses?
En el último paso del proceso se contestarán estas y otras preguntas más.
Figura 9
Perfil del tiempo de terminación del proyecto
3.7. Séptimo paso: Análisis de sensibilidad probabilístico.
El árbol de decisiones desarrollado (Figura 5) no solo permite establecer el perfil del TTP del proyecto (Figura 9), sino también obtener información adicional que ayude a entender mejor los posibles tiempos de terminación del proyecto.
Se pueden establecer distribuciones y tiempos esperados (VE) del TTP en nodos distintos al primero del árbol y ver cómo varían estos valores condicionales. Es decir, se puede realizar un análisis de sensibilidad probabilístico de los tiempos de duración de las actividades del proyecto fijando uno de ellos en un valor dentro de su rango y permitiendo que los tiempos de las otras actividades varíen de acuerdo con sus respectivas distribuciones de probabilidades.
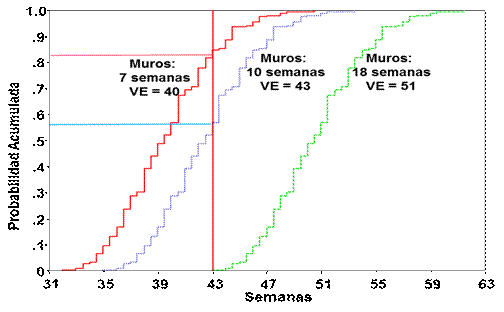
Este análisis ayuda a comprender mejor el riesgo de no terminar el proyecto en un tiempo preestablecido. Se busca establecer las distribuciones de probabilidades asociadas con los diferentes valores de los tiempos de las actividades del proyecto. Por ejemplo, se pueden determinar las distribuciones condicionales a los diferentes tiempos de la actividad de levantamiento de muros; esto es, 7, 10 y 18 semanas. Estas distribuciones condicionales se presentan en la Figura 10, donde se observa que el perfil del TTP es muy sensible al tiempo del levantamiento de muros. A medida que este tiempo aumenta, el TTP esperado (VE) se incrementa de 40 a 51 semanas. Además, si el tiempo de los muros tomara 18 semanas, la probabilidad de cumplir con la meta de 43 semanas es cero; pero si este tiempo se redujera a 7, esta probabilidad se eleva al 83%.
Figura 10
Distribuciones de probabilidades condicionales del TTP al tiempo de duración de la actividad levantamiento de muros
También se pueden establecer las distribuciones de probabilidades condicionales para otros nodos de azar del árbol (tiempos de las actividades). Por ejemplo, se pueden determinar las distribuciones de probabilidades condicionales del TTP para el tiempo de duración de la actividad de cimentación, colocando el nodo de azar que representa esta incertidumbre antes que los otros nodos de azar en el árbol de decisiones y ubicándolo después del nodo de decisión.
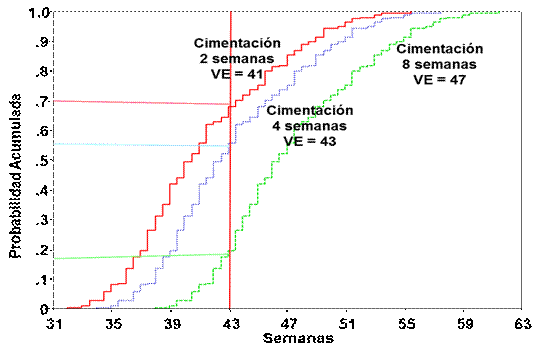
Las distribuciones de probabilidades condicionales para el tiempo de cimentación se presentan en la Figura 11, donde se muestra que el perfil del TTP también es sensible al tiempo de cimentación. A medida que este tiempo aumenta, el TTP esperado (VE) se incrementa de 41 a 47 semanas. Además, si el tiempo de cimentación tomara 8 semanas, la probabilidad de cumplir con la meta de 43 semanas es del 18 %; pero si este tiempo se redujera a 2 semanas, esta probabilidad se eleva al 70 %.
Figura 11
Distribuciones de probabilidades condicionales del TTP al tiempo de duración de la actividad cimentación
De igual manera, es posible establecer las distribuciones de probabilidades condicionales para los otros nodos de azar del árbol. En la Tabla 6 se muestran los resultados del análisis de sensibilidad probabilístico para cada uno de los tiempos de las actividades críticas del proyecto. La penúltima columna expone el cambio en el TTP esperado (VE), que está dado por la diferencia entre el TTP esperado asociado al tiempo alto y al tiempo bajo de culminación de cada actividad. La última columna muestra la probabilidad de terminar el proyecto en 43 semanas asociada al tiempo más alto de culminación de cada actividad.
Tabla 6
Resumen del análisis de sensibilidad probabilística

Tras realizar este análisis de sensibilidad probabilístico, se puede responder a la pregunta: “¿Cuán importante es el tiempo de terminación de una actividad crucial cuando se permite que los tiempos de culminación de las otras actividades cruciales varíen probabilísticamente?”. De las distribuciones de probabilidad condicionales y los TTP esperados, se concluye que todas las actividades son cruciales, pues los TTP varían en al menos 4 semanas, dependiendo de los tiempos particulares que tomen estas actividades. Sin embargo, el tiempo de terminación de la actividad de levantamiento de muros produce la mayor variación en el TTP esperado (11 semanas), y la probabilidad de terminar el proyecto antes de las 43 semanas es cero cuando el tiempo para culminar esta actividad alcanza su valor máximo.
3.8. Octavo paso: Resumen y conclusiones
El perfil del proyecto (Figura 9) y el análisis probabilístico permiten responder a muchas preguntas de las partes interesadas, como las planteadas al comienzo de este artículo:
· ¿Cuál es el tiempo esperado de culminación del proyecto?
Del perfil del TTP, se observa que el tiempo esperado de culminación del proyecto es de 44 semanas.
· ¿Cuál es el rango de incertidumbre en la fecha de término del proyecto?
El perfil del TTP del proyecto tiene una incertidumbre de 30 semanas, lo que significa que terminar el proyecto puede tomar entre 32 y 62 semanas.
· ¿Cuál es la probabilidad de que el proyecto se termine en 43 semanas?
Al observar la Figura 9, se ve que hay una probabilidad del 49 % de que el proyecto se termine en 43 semanas o menos. La pregunta es si estamos dispuestos a establecer en la propuesta que el proyecto se terminará en 43 semanas, asumiendo el riesgo del 51 % de no culminarlo en ese tiempo y recibir la multa alta establecida en el contrato.
· ¿Debe incluirse este proyecto en el portafolio de obras de la organización para el próximo año?
Esta respuesta depende de lo atractivo de los otros proyectos en el portafolio y de la actitud al riesgo de la organización. Si la organización está dispuesta a aceptar un 51 % de probabilidad de no terminar el proyecto en 43 semanas, requeridas en el contrato, debe incluirlo en su portafolio.
· ¿Cuán sensible es el perfil de TTP a los tiempos inciertos de las diferentes actividades críticas?
Del análisis de sensibilidad probabilístico, se concluye que el perfil es sensible a los tiempos de las cinco actividades críticas, especialmente al tiempo de culminación del levantamiento de muros. Las distribuciones de probabilidades condicionales y los TTP esperados (VE) varían dependiendo del tiempo que tomen en culminar estas actividades. En el caso de la actividad del levantamiento de los muros, si ésta se demora 18 semanas (su tiempo mayor), la probabilidad de terminar el proyecto antes de las 43 semanas es cero. La pregunta es: ¿qué podemos hacer para asegurarnos de que el tiempo de culminación del levantamiento de muros sea lo menor posible?
4. CONCLUSIONES Y RECOMENDACIONES
El procedimiento propuesto para estimar probabilísticamente el tiempo de puesta en marcha de los proyectos se basa en el reconocimiento explícito de que ningún experto tiene información completa sobre la duración de las diferentes actividades del proyecto y, por tanto, del tiempo de culminación de este (Tversky & Kahneman, 1974). Utilizar probabilidades para describir la incertidumbre respecto al tiempo de las actividades ayuda a mejorar la comunicación entre los diferentes expertos, facilitando el intercambio de información de manera explícita y evitando sesgos motivacionales y cognitivos[5].
Para describir la relación entre las actividades que conforman el proyecto, se emplea la red PERT, un método validado en diversos tipos de proyectos y niveles de complejidad durante más de 60 años. El aporte del procedimiento aquí propuesto es la incorporación explícita de la incertidumbre en los tiempos de cada una de las actividades. Además, se presenta una manera sencilla y bien estructurada de modelar la red PERT en una hoja de cálculo, lo cual permite realizar un análisis probabilístico utilizando el software especializado Supertree®.
El resultado final permitirá a las diferentes partes interesadas definir los proyectos de un portafolio (por ejemplo, de un plan de obras), visualizar explícitamente el grado de incertidumbre en el tiempo de puesta en marcha de dichos proyectos e identificar las actividades clave que generan esta incertidumbre en el TTP. De este modo, se podrán identificar acciones para reducir el riesgo de no cumplir con la fecha preestablecida, promoviendo una gestión proactiva del riesgo.
REFERENCIAS
Anderson, D.R., Sweeney D. J., Williams T.A.(2015). Quantitative Methods for Business. Cengage Learning
Howard, R.A. (1966). Decision Analysis: Applied Decision Theory. Proceedings of the Fourth International Conference in Operational Research. Reprinted in Howard, R.A., & Matheson, J. E. (1984).
Munier, R.A. (1981). PERT-CPM y técnicas relacionadas. Editorial Astrea.
Salinas Ortiz, J. A. (2009). Análisis de decisiones estratégicas en entornos inciertos, cambiantes y complejos. Buenos Aires: Cengage Learning.
Salinas Ortiz, J. A. (2004). Análisis Probabilístico del Plan de Obras para la determinación de las Tarifas Eléctricas. Reporte de un trabajo de consultoría hecho para la OSINERG.
Supertree Software. (s.f.). Supertree and Sensitivity are trademarks of SmartOrg, Inc. https://smartorg.com/supertree-sensitivity/.
Tversky, A. & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases. Science, 211, 453-458.