Revista IECOS, 25(2), 77-103 | Julio-Diciembre 2024 | ISSN 2961-2845 | e-ISSN 2788-7480
MODELOS SEMI-MÁRKOV PARA LA EVALUACIÓN DEL TIEMPO, LUGAR, MAGNITUD Y PROFUNDIDAD DE LOS SISMOS OCURRIDOS EN EL SUR DEL PERÚ 2023
SEMI-MARKOV MODELS FOR THE EVALUATION OF TIME, PLACE, MAGNITUDE AND DEPTH OF EARTHQUAKES IN SOUTHERN PERU 2023
Carlos Risco Franco![]() 1,
Joel Salomon Rios Nima
1,
Joel Salomon Rios Nima ![]() 2,
Marlene Angela Payano Mendez
2,
Marlene Angela Payano Mendez![]() 3
3
1Universidad Nacional de Ingeniería, Lima, Perú
2Universidad Nacional de Ingeniería, Lima, Perú
3Universidad Nacional de Ingeniería, Lima, Perú
E-mail: 1crisco@uni.edu.pe, 2jordan.poma.c@uni.pe, 3marlene.payano.m@uni.pe
1https://orcid.org/0000-0003-1323-436X, 2https://orcid.org/0009-0001-0799-5536, 3https://orcid.org/0009-0004-2883-838X
https://doi.org/10.21754/iecos.v25i2.2196
Recibido (Received): 24/03/2024 Aceptado (Accepted): 21/08/2024 Publicado (Published): 27/09/2024
RESUMEN
El Perú se sitúa en la región sísmica del Pacífico Sur y experimenta con frecuencia sismos significativos. Entre los eventos más relevantes se encuentran el sismo de 8.4 grados de magnitud ocurrido en Arequipa en el año 2001, el sismo de magnitud 7.9 en Ica en agosto de 2007 y nuevamente un sismo de magnitud 6.3 en Arequipa en julio de 2017. Estos eventos subrayan la necesidad de realizar estudios de riesgo sísmico en la región.
Este estudio es de tipo descriptivo y correlacional, con un diseño transversal, cuyo objetivo es identificar las áreas en el sur del Perú con mayor riesgo de experimentar sismos de alta magnitud. Los datos provienen del Instituto Geofísico del Perú y abarcan el periodo de 1960 a 2023, analizando sismos con magnitud igual o superior a 5.5 Mw. Se aplicó la metodología de (Sadeghian, 2012), basada en el modelo semi-Márkov, para predecir tiempo y ubicación de eventos sísmicos, extendiendo este modelo también a los estados de la profundidad. Se destacan las zonas de Pisco-Ica y Chala-Atico como las de mayor riesgo para la ocurrencia de sismos de gran magnitud.
Palabras clave: Sismo, semi-Márkov, Clúster Análisis.
ABSTRACT
Peru is located in the seismically active South Pacific region and frequently experiences significant earthquakes. Among the most notable events are the 8.4-magnitude earthquake in Arequipa in 2001, the 7.9-magnitude earthquake in Ica in August 2007, and another 6.3-magnitude earthquake in Arequipa in July 2017. These events underscore the need for seismic risk studies in the region.
This study is descriptive and correlational, with a cross-sectional design, aiming to identify the areas in southern Peru with the highest risk of experiencing high-magnitude earthquakes. The data comes from the Geophysical Institute of Peru and covers the period from 1960 to 2023, analyzing earthquakes with a magnitude of 5.5 Mw or higher. The methodology of Sadeghian (2012), based on the semi-Markov model, was applied to predict the time and location of seismic events, extending this model to the states of depth as well. The Pisco-Ica and Chala-Atico zones are highlighted as having the highest risk for high-magnitude earthquakes.
1. INTRODUCCIÓN
América del Sur, incluyendo Perú, forma parte del Cinturón de Fuego del Pacífico, una región donde la tierra libera más del 85% de su energía a través de terremotos y erupciones volcánicas. Este alto índice de sismicidad se debe a que en el borde Oeste de América del Sur se produce la colisión entre las placas de Nazca y Sudamérica, la primera más débil se introduce por debajo de la segunda originando el proceso conocido como subducción, el mismo que se constituye en la principal fuente generadora de terremotos en el Perú (Tavera, 2001).
En los últimos 20 años, el sur del Perú ha experimentado varios sismos de alta magnitud, mencionaremos dos de ellos.
El 23 de junio de 2001, un terremoto de magnitud 7.9 Mw afectó toda la región sur de Perú, incluyendo las ciudades de Arica e Iquique en Chile, así como La Paz en Bolivia. El epicentro del terremoto fue localizado en la región sur, cerca de la línea de costa, específicamente a 80 km al noroeste de la localidad de Ocoña en el departamento de Arequipa (Tavera et al., 2001).
El último gran sismo generado por el proceso de convergencia de placas ocurrió el 15 de agosto de 2007, con una magnitud de 7.9 Mw, conocido como el 'sismo de Pisco' debido a que su epicentro se ubicó a 60 km al oeste de esta ciudad. El sismo causó daños significativos en aproximadamente el 80% de las viviendas de Pisco y afectó de manera menor a localidades cercanas. Además, generó un tsunami que se originó frente a las localidades al sur de la península de Paracas. (Tavera et al., 2007).
Por lo tanto, es evidente la necesidad de prevenir eventos sísmicos y también de identificar los lugares con mayor riesgo de sismos de alta magnitud, lo que permitiría priorizar recursos para la prevención, preparación y alerta de la población del país.
En la literatura se encuentra disponible una amplia gama de modelos estadísticos para la ocurrencia de terremotos. Por ejemplo, el modelo de Poisson proporciona un enfoque típico para una serie aleatoria de eventos. Este modelo asume que las ocurrencias de terremotos son eventos independientes en el espacio y tiempo. Sin embargo, esta función "sin memoria" no es adecuada para este tipo de eventos. Un nuevo enfoque basado en modelos semi-Markov permite tomar en consideración la suposición más realista de la dependencia de los eventos en el espacio y el tiempo. Por ejemplo, la probabilidad de ocurrencia de un terremoto (en la misma zona sísmica) depende de la magnitud del evento anterior, así como del tiempo transcurrido (Masala, 2012).
Masala (2012), aplica el modelo semi-Markov de tiempo discreto, para estimar la ocurrencia de los terremotos. Y utiliza las ecuaciones de evolución, cuya solución le permite determinar las probabilidades de intervalo. Además, para la distribución de los tiempos de espera, considera un modelo paramétrico y utiliza la Distribución de Weibull Generalizada.
Sadegian (2012) también aplica el modelo semi-Markov a datos de Sismos y señala, “en nuestro trabajo dividimos la provincia de Teherán en seis regiones, y por otro lado aplicó el modelo semi-Markov a intervalos de la magnitud, para ello agrupó los terremotos según su magnitud en tres clases. Finalmente utilizando el modelo semi-Markov, procede a predecir la probabilidad del lugar de ocurrencia de sismos en la provincia de estudio.
Altinok y Kolcak (1999) aplican la teoría semi-Markov (método no paramétrico) al modelo, sobre sismos ocurridos en el norte de la falla Anatolian entre 1902 y 1992. Ellos asumen que dos sismos consecutivos ocurridos en la misma zona de discontinuidad estructural no son eventos independientes, pero ellos dependen del intervalo de tiempo entre ellos. Además, ellos obtienen las probabilidades de ocurrencia, determinando las probabilidades de transición de región a región y transiciones de magnitud a magnitud de esos sismos.
Garavaglia y Pavani (2011), proponen un proceso de renovación de Markov, y para modelar los tiempos de espera, proponen una mezcla de distribuciones exponencial y Weibull, se estiman sus parámetros siguiendo el método de máxima verosimilitud. Validan su modelo utilizando datos de terremotos de alta gravedad ocurridos en Turquía durante el siglo XX. Según ellas, los resultados muestran una buena concordancia con los hechos reales.
Alvarez (2005) también aplica un modelo de renovación. Afirma que las distribuciones de los tiempos de espera dependen sólo en los tipos del último y siguiente evento. En lo que respecta a los tiempos de espera, el autor propone la distribución de Weibull dentro de un enfoque paramétrico. Los parámetros y las probabilidades de transición se estiman mediante el método clásico de máxima verosimilitud. Finalmente, el modelo lo prueba con una base de datos de terremotos de tres tipos de gravedad ocurridos en Turquía durante el siglo XX.
Como se puede observar, el uso del modelo semi-Márkov se justifica debido a su aplicación previa en la evaluación de riesgos y pronósticos de la ocurrencia de sismos, en contraste con la consideración de otros modelos como el proceso Poisson o el proceso de Márkov, los cuales se han descartado por no ser adecuados para este caso específico de evaluación sísmica.
El objetivo principal de este proyecto es identificar una zona en la región sur del Perú con alta probabilidad de ocurrencia de sismos de gran magnitud y profundidad superficial, para luego elaborar pronósticos para un período de tiempo determinado.
En este estudio, se utilizó la información sobre los sismos ocurridos en el sur del Perú desde 1960 hasta junio de 2023, obtenida del sitio web del Instituto Geofísico del Perú (IGP).
Mi agradecimiento sincero al Instituto de Estudios Económicos y Sociales (IECOS), en particular a su director el Mg. Rafael Vásquez y al personal administrativo por el apoyo constante para la culminación del presente artículo.
2. MÉTODOLOGÍA
2.1 TIPO DE INVESTIGACIÓN
El estudio es de tipo correlacional, ya que el modelo semi-Márkov asume una dependencia temporal entre sismos consecutivos, así como en los periodos de permanencia en diferentes zonas geográficas, magnitudes y profundidades.
El estudio es de corte longitudinal, porque se estudia en un periodo de tiempo, de las variables ubicación geográfica, magnitud y profundidad, desde 1960 hasta junio del 2023.
2.2 POBLACIÓN Y MUESTRA
Un proceso estocástico se define como una colección de variables aleatorias que evolucionan en el tiempo Xt, t representa el tiempo, tomando valores en un conjunto E de estados. Para ilustrarlo, es similar al electrocardiograma que un médico utiliza de un paciente en un momento específico para diagnosticar el funcionamiento del corazón. El médico debe diagnosticar basándose únicamente en una realización del proceso estocástico, que representa gráficamente el comportamiento del corazón del paciente en ese momento.
De manera análoga, la magnitud de los sismos se registra cada vez que estos ocurren. Tenemos registros de sismos desde 1960 hasta 2023, y su representación gráfica es comparable a un electrocardiograma de un paciente. Es por esto, por lo que en un proceso estocástico no se aplica el concepto de población y muestra, ya que no es posible retroceder en el tiempo y obtener otro registro del mismo proceso.
2.3 IDENTIFICACIÓN DE VARIABLES
Las variables consideradas en este estudio son las siguientes:
- Fecha del sismo: indica el día, mes y año en que ocurrió.
- Hora del sismo: momento exacto en que se produjo el sismo, especificado en horas, minutos y segundos.
- Ubicación geográfica del sismo: se refiere al lugar exacto donde ocurrió el sismo, determinado por su latitud y longitud.
La latitud es la distancia angular entre un punto específico de la Tierra y la línea ecuatorial, medida a lo largo del meridiano en el que se encuentra dicho punto. Dependiendo del hemisferio en el que se sitúe el punto, puede ser latitud norte o sur.
Por otro lado, la longitud mide el ángulo a lo largo del ecuador terrestre desde cualquier punto hasta el meridiano de Greenwich en Londres, que se acepta como longitud 0 en la mayoría de las sociedades modernas. Las líneas de longitud son círculos máximos que atraviesan los polos y se conocen como meridianos.
La magnitud del sismo se determina mediante la escala de magnitud de momento (denotada como Mw), la cual evalúa el tamaño de los terremotos en función de la energía liberada durante el evento. Esta medida específicamente representa el momento del terremoto, definido como la rigidez de la Tierra multiplicada por el deslizamiento promedio en la falla y el tamaño del área que se movió (Masala, 2012).
Por otro lado, la profundidad del sismo se refiere a la distancia medida en kilómetros desde la superficie hasta la falla donde ocurrió el sismo.
2.4 EL MODELO SEMI-MARKOV
El modelo semi-markov, se define de
la siguiente manera (Janssen & Manca, 2006). En un espacio de probabilidad ![]() , dadas las
variables aleatorias
, dadas las
variables aleatorias
![]()
El proceso ![]() es
un proceso semi-Markov de tiempo discreto si la matriz Q asociada con el
proceso homogéneo, viene dado por
es
un proceso semi-Markov de tiempo discreto si la matriz Q asociada con el
proceso homogéneo, viene dado por
![]()
Introducimos la matriz de transición P del proceso de Markov subyacente de la siguiente manera:
![]()
Definimos la probabilidad de que el proceso abandone el estado i dentro de un tiempo t como:
![]()
La siguiente relación también es válida:
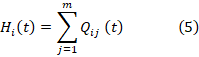
Introduzcamos las siguientes probabilidades que son específicas del caso discreto homogéneo:
![]()
De la definición de Q obtenemos inmediatamente:
![]()
La función de distribución condicional de los tiempos de espera, dado el estado actual y el estado siguiente, viene dado por:
![]()
Las siguientes relaciones se pueden deducir fácilmente:
![]()
Algoritmo para resolver las ecuaciones de evolución en el caso homogéneo:
Fijemos un horizonte de tiempo [0, T] y una subdivisión finita con intervalos de longitud h.
Los datos de entrada son la matriz
de transición P y las distribuciones de tiempo de espera ![]() .
Las matrices F son mxm (m denota el número de estados) y deben evaluarse para
t=1, …, k usando las distribuciones previamente determinadas, establecemos la
relación evidente F(0)=0.
.
Las matrices F son mxm (m denota el número de estados) y deben evaluarse para
t=1, …, k usando las distribuciones previamente determinadas, establecemos la
relación evidente F(0)=0.
Las matrices Q se definen como Q(t) = F(t) x P (producto “elemento por elemento”) (10)
Las matrices B están dadas por
![]()
Deducimos entonces las matrices H de la siguiente manera:
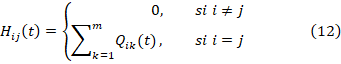
Estas matrices representan la probabilidad de salir del estado i dentro del tiempo t. Esto es representan la probabilidad que ocurra un sismo en el estado i, en el tiempo t.
Lo contrario a lo anterior, representa la matriz D definida por D(t) = I – H(t). (13)
La probabilidad que no ocurra un sismo en el tiempo t.
2.5 CLUSTER ANALISIS
La teoría del análisis de conglomerados, especialmente los métodos jerárquicos, se ha basado en el trabajo de L. Kaufman y P. Rousseeuw (2005):
Los métodos jerárquicos, son técnicas de agrupamiento que construye una jerarquía de clusters. En lugar de requerir un número predefinido de clusters como en otros métodos, este método genera una estructura en forma de árbol o dendrograma que muestra cómo los clusters se fusionan o dividen en cada etapa del proceso.
Principales características y pasos del método jerárquico son:
Medida de similitud: Se elige una medida de similitud entre los objetos, como la distancia euclidiana, la correlación, etc. Esta medida determina cuán cercanos o similares son dos objetos.
Construcción del dendrograma: Se comienza con cada objeto como un cluster individual y se van fusionando gradualmente los clusters más cercanos o separando los menos similares, según la medida de similitud elegida. Este proceso se representa gráficamente en un dendrograma, que es un árbol que muestra la secuencia de fusiones y divisiones.
Elección del método de enlace: Existen diferentes métodos de enlace que determinan cómo se calcula la distancia entre clusters para decidir cuáles fusionar en cada paso. Algunos métodos comunes son el enlace simple, completo (o máximo), promedio y el enlace de Ward, entre otros.
Corte del dendrograma: Para obtener un número específico de clusters, se realiza un corte en el dendrograma a una altura determinada. La elección de este punto de corte puede hacerse visualmente o mediante criterios específicos, como la máxima discrepancia o coherencia interna de los clusters resultantes.
2.6 PROCEDIMIENTO PARA LA APLICACIÓN DEL MODELO SEMI-MARKOV
Para ejecutar el presente trabajo, se precedió de la siguiente manera.
Se identificaron las cinco zonas geográficas con mayor concentración de sismos utilizando las variables de latitud y longitud mediante el análisis de conglomerados o Cluster Analysis, método gerárquico, con medida de similitud la distancia euclideana, método de enlace el promedio y el corte del dendrograma se realizó visualmente buscando obtener diez grupos. Inicialmente se exploraron estos diez grupos, de los cuales se seleccionaron solo aquellos con la mayor concentración de sismos. Estas cinco zonas, en el modelo semi-Márkov, se consideran como estados.
Para aplicar el modelo semi-Márkov, primero se estima la matriz de transición P. Esta matriz es constante debido a que se trata de un modelo semi-Márkov homogéneo, donde las probabilidades de transición se mantienen constantes a lo largo del tiempo.
En el siguiente paso, se determinan los parámetros que describen la distribución de los tiempos de espera de cada transición.
Para este propósito, extraemos de nuestra base de datos los tiempos de espera empíricos y aplicamos la distribución de Weibull o Gamma, según cuál se ajuste mejor a los datos. Los parámetros de la distribución de los tiempos de espera de cada transición se estiman mediante el método de máxima verosimilitud (Masala, 2012).
Finalmente, se estiman las matrices para calcular las probabilidades de intervalo de tiempo y realizar los pronósticos correspondientes.
Además, se aplica el modelo semi-markov a la magnitud de los sismos, clasificándolos en tres intervalos o estados, lo que permite 9 posibles transiciones. El procedimiento es similar al aplicado en el caso de las zonas geográficas.
Igualmente, se aplica el modelo semi-markov a la profundidad de los sismos, dividiéndola en tres intervalos o estados, lo que también permite 9 posibles transiciones. Posteriormente, se sigue un procedimiento similar al aplicado en el caso de las zonas geográficas.
Finalmente, combinando los resultados anteriores, llevamos a cabo las predicciones para la zona con mayor riesgo de ocurrencia de sismos de alta magnitud (Magnitud > 5) y sismos superficiales (Profundidad < 60 km), que son de especial interés debido a su peligrosidad y al potencial de causar mayores daños.
Para realizar los cálculos se utilizaron los softwares, SPSS, R, Excel y Google EathPro.
3. RESULTADOS Y DISCUSIÓN
Para identificar las zonas de mayor actividad sísmica, se utilizaron los datos de sismos publicados regularmente por el ICC en su página web, abarcando el periodo desde enero de 1960hasta junio del 2023, con una magnitud igual o mayor a 3. Para la aplicación del modelo semi-Márkov, se consideraron únicamente los sismos con magnitudes iguales o superiores a 5.5 en las mismas fechas y limitados a las 5 zonas geográficas identificadas previamente.
3.1 RESULTADOS DESCRIPTIVOS DE LOS SISMOS DEL SUR DEL PERÚ
La magnitud de los sismos.
Figura 1: Frecuencia de la magnitud de los sismos
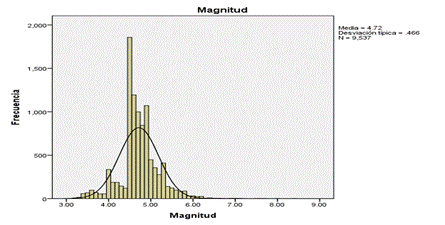
Fuente: Elaboración propia. Datos IGP.
Como se puede observar en la Figura Nº 1, la mayoría de los sismos se concentran en magnitudes entre 4.5 y 5.0 Mw. Sin embargo, también se observa la presencia de sismos con magnitudes superiores a 6.0 Mw, los cuales pueden ser catalogados como terremotos.
La profundidad de los sismos – características generales
Figura 2: Frecuencia de la profundidad de los sismos
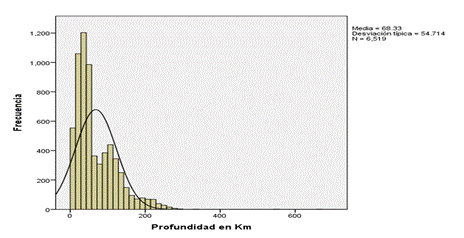
Fuente: Elaboración propia. Datos IGP.
Como se puede apreciar en la Figura 2, se observa un considerable número de sismos con profundidades inferiores a 60 km, los cuales son conocidos por su capacidad destructiva al tratarse de sismos superficiales.
Tabla 1 Valores descriptivos para los sismos del sur del Perú
|
Estadísticos |
Profundidad en Km |
Magnitud Mw |
|
Media |
68.33 |
4.7818 |
|
Mediana |
48 |
4.7 |
|
Desv. estándar |
54.714 |
0.38569 |
|
Mínimo |
5 |
4 |
|
Máximo |
661 |
8.4 |
|
Válidos |
6519 |
6519 |
|
Perdidos |
0 |
0 |
Fuente: Elaboración propia. Datos IGP.
Como se muestra en la tabla 1, la profundidad media de los sismos es de 68 km, con una desviación estándar de 54.71 km. Esto implica que aproximadamente el 50% de los sismos se localizan por debajo de esta profundidad, lo cual corresponde a los sismos superficiales, conocidos por ser los más destructivos.
La media de la magnitud es de 4.7 Mw. Nos preocupa que aproximadamente el 50% de los sismos tengan magnitudes superiores a esta media pues corresponde a sismos de alta magnitud.
3.2 IDENTIFICACIÓN DE LAS ZONAS SÍSMICAS
Los datos han sido obtenidos de la página web del Instituto Geofísico del Perú, IGP. (IGP, 2023)
Los sismos del sur del Perú han sido considerados aquellos que se encuentran dentro de las coordenadas Latitud desde -13.001 (que corresponde a la ciudad de Chincha) hasta la latitud -19.49 que corresponde al grupo de sismos alrededor de la ciudad de Tacna, en los cuales se incluyen algunos sismos alrededor de la ciudad de Arica en el norte de Chile. Y respecto a las longitudes consideradas, los sismos con longitudes desde -69.27 hasta -77.63. Además, se han considerado los sismos con magnitud mayor o igual a 3.
Para asegurar la replicabilidad del presente estudio, es crucial considerar los datos proporcionados por el IGP correspondientes a las latitudes y longitudes mencionadas en el párrafo anterior, así como la base de datos que incluye los sismos de las 5 zonas identificadas con mayor frecuencia. Estos sismos deben cumplir con la condición de tener magnitudes iguales o superiores a 5.5 Mw, los cuales fueron utilizados para aplicar el modelo semi-Márkov a los estados geográficos, así como a la magnitud y profundidad de los sismos.
Para identificar las áreas con mayor concentración de sismos, se utilizó la herramienta estadística CC, aplicando variables de latitud y longitud con distancia euclidiana y método promedio dentro de los grupos. Se obtuvieron N grupos, de los cuales se seleccionaron arbitrariamente n grupos que muestran una mayor concentración de sismos de manera gráfica, los cuales fueron incluidos en el estudio, mientras que los demás no se consideraron. Las zonas identificadas se presentan a continuación.
Tabla 2 Zonas sísmicas identificadas con mayor actividad sísmica en el sur del Perú
|
Zona 1 |
Maca – Sallalli |
|
Zona 2 |
Pisco - Ica |
|
Zona 3 |
Chala - Atico |
|
Zona 4 |
Tacna - Tarata |
|
Zona 5 |
Mollendo - Camana |
Fuente: Elaboración propia. Datos IGP.
A continuación, se muestran las figuras de las zonas geográficas, donde los sismos están representados como puntos, utilizando el programa Google EathPro y las bases de datos correspondientes.
Figura 3: Zona 1: Maca – Sallalli
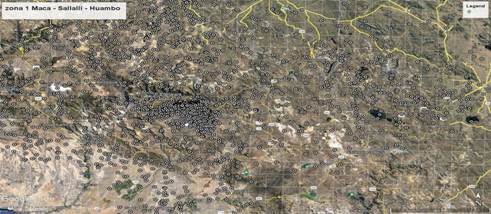
Fuente: Elaboración propia. Datos IGP.
Figura 4: Frecuencia de la Magnitud de los sismos de la Zona 1 Maca-Sallalli
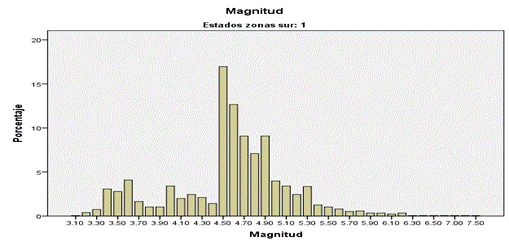
Fuente: Elaboración propia. Datos IGP.
Figura 5: Zona 2 Pisco – Ica

Fuente: Elaboración propia con Google EarthPro. Datos IGP.
Figura 6: Frecuencia de la Magnitud de los sismos de la Zona 2 Pisco-Ica
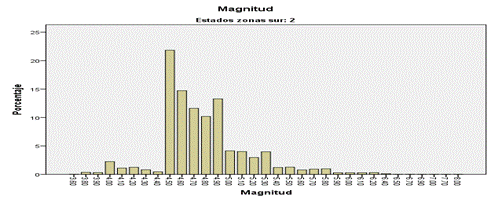
Fuente: Elaboración propia. Datos IGP.
Figura 7: Zona 3 Chala – Atico

Fuente: Elaboración propia. Datos IGP.
Figura 8 Frecuencia Magnitud de los sismos de la Zona 3 Chala – Atico
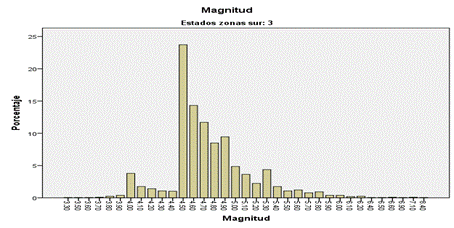
Fuente: Elaboración propia. Datos IGP.
Figura 9 Zona 4 Tacna-Tarata
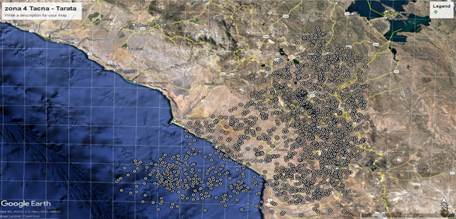
Fuente: Elaboración propia. Datos IGP.
Figura 10 Magnitud de los sismos de la Zona 4 Tacna-Tarata
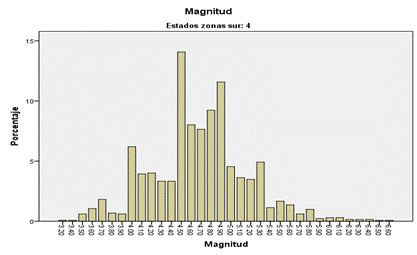
Fuente: Elaboración propia. Datos IGP.
Figura 11 Zona 5 Mollendo – Camaná
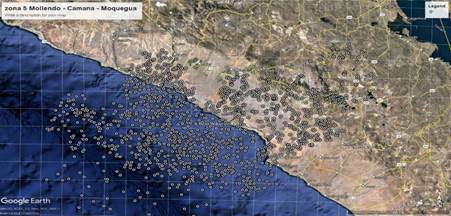
Fuente: Elaboración propia. Datos IGP.
Figura 12 Magnitud de los sismos de la Zona 5 Mollendo-Camaná
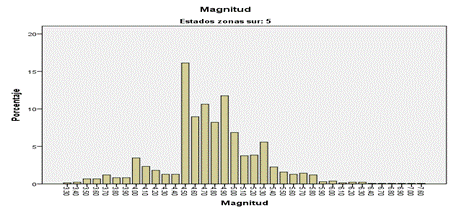
Fuente: Elaboración propia. Datos IGP.
Como se puede observar en la Figura 12, se nota un aumento significativo en el porcentaje de sismos de magnitud 4.4 Mw a 4.5 Mw, manteniéndose alto hasta alcanzar una magnitud de 5.3 Mw. Además, se registran sismos con magnitudes entre 6.0 Mw y 7.6 Mw, los cuales se consideran como terremotos.
3.3 APLICACIÓN DEL MODELO SEMI-MARKOV A LAS ZONAS GEOGRÁFICAS IDENTIFICADAS
Para la aplicación del modelo semi-Markov, se consideraron los sismos con magnitud mayor o igual a 5.5 Mw, de las 5 zonas geográficas identificadas en el punto anterior.
Tabla 3: Matriz de transición de las zonas geográficas
|
Estados |
Maca-Sallalli |
Pisco-Ica |
Chala-Atico |
Tacna-Tarata |
Mollendo-Camaná |
|
Maca-Sallalli |
0.1688 |
0.2857 |
0.2597 |
0.1558 |
0.1299 |
|
Pisco-Ica |
0.2155 |
0.2759 |
0.1724 |
0.1724 |
0.1638 |
|
Chala-Atico |
0.1262 |
0.2330 |
0.2621 |
0.2039 |
0.1748 |
|
Tacna-Tarata |
0.1842 |
0.2763 |
0.2105 |
0.1579 |
0.1711 |
|
Mollendo-Camaná |
0.1571 |
0.2429 |
0.3000 |
0.1571 |
0.1429 |
Fuente: Elaboración propia. Datos IGP.
Cálculo de los parámetros de las distribuciones de los tiempos de espera para cada transición, Weibull (W) o Exponencial, según corresponda el mejor ajuste.
Figura 13: Distribución de Weibull para los tiempos de permanencia en la transición t11
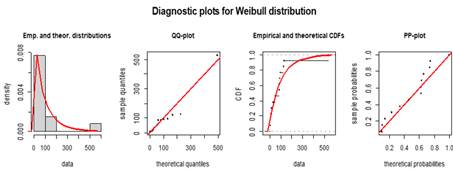
Fuente: Elaboración propia. Datos IGP.
Tabla 4 Parámetros de forma y escala de las distribuciones de los tiempos de espera
|
Transiciones |
Param. Forma |
Param. Escala |
Distribucion |
|
t11 |
0.8584378 |
89.1998131 |
weibull |
|
t12 |
1.219276 |
73.510288 |
weibull |
|
t13 |
0.8810227 |
76.1155414 |
weibull |
|
t14 |
0.7755798 |
71.5592617 |
weibull |
|
t15 |
0.5995549 |
41.2208355 |
weibull |
|
t21 |
1.087901 |
80.155344 |
weibull |
|
t22 |
0.02066156 |
|
Exponencial |
|
t23 |
1.262244 |
38.744752 |
Weibull |
|
t24 |
1.551228 |
63.134962 |
Weibull |
|
t25 |
1.200646 |
50.091955 |
Weibull |
|
t31 |
1.582026 |
74.393902 |
Weibull |
|
t32 |
0.8679904 |
65.8911397 |
Weibull |
|
t33 |
0.9191447 |
58.7440574 |
Weibull |
|
t34 |
0.9887603 |
39.9986462 |
Weibull |
|
t35 |
1.120683 |
46.396619 |
Weibull |
|
t41 |
0.8073415 |
43.2033854 |
Weibull |
|
t42 |
1.153229 |
60.40362 |
Weibull |
|
t43 |
1.095177 |
49.90906 |
Weibull |
|
t44 |
1.169947 |
101.961268 |
Weibull |
|
t45 |
0.01122712 |
|
Exponencial |
|
t51 |
1.018869 |
62.59436 |
Weibull |
|
t52 |
0.7381157 |
68.2313454 |
Weibull |
|
t53 |
0.7950644 |
40.1406398 |
Weibull |
|
t54 |
1.120759 |
62.051584 |
Weibull |
|
t55 |
0.6976586 |
53.926287 |
Weibull |
Fuente: Elaboración propia. Datos IGP.
Tabla 5 Cálculo de las probabilidades de acuerdo con las distribuciones de los tiempos de espera, Fij(t), para t=1 mes
|
Estados |
Maca-Sallalli |
Pisco-Ica |
Chala-Atico |
Tacna-Tarata |
Mollendo-Camaná |
|
Maca-Sallalli |
0.3246 |
0.2849 |
0.3562 |
0.3992 |
0.5624 |
|
Pisco-Ica |
0.2906 |
0.4620 |
0.5152 |
0.2704 |
0.4175 |
|
Chala-Atico |
0.2116 |
0.3966 |
0.4168 |
0.5288 |
0.4585 |
|
Tacna-Tarata |
0.5252 |
0.3599 |
0.4360 |
0.2126 |
0.2860 |
|
Mollendo-Camaná |
0.3767 |
0.4203 |
0.5477 |
0.3578 |
0.4853 |
Fuente: Elaboración propia. Datos IGP.
Tabla 6 Cálculo de las probabilidades de acuerdo con las distribuciones de los tiempos de espera, Fij(t), para t= 3 meses
|
Estados |
Maca-Sallalli |
Pisco-Ica |
Chala-Atico |
Tacna-Tarata |
Mollendo-Camaná |
|
Maca-Sallalli |
0.6349 |
0.7219 |
0.6862 |
0.6972 |
0.7975 |
|
Pisco-Ica |
0.6784 |
0.8443 |
0.9448 |
0.8233 |
0.8675 |
|
Chala-Atico |
0.7412 |
0.7304 |
0.7724 |
0.8924 |
0.8777 |
|
Tacna-Tarata |
0.8361 |
0.7948 |
0.8515 |
0.5786 |
0.6359 |
|
Mollendo-Camaná |
0.7649 |
0.7068 |
0.8505 |
0.7806 |
0.7606 |
Fuente: Elaboración propia. Datos IGP.
Tabla 7 Cálculo de Q1 para t = 1 mes
|
Estados |
Maca-Sallalli |
Pisco-Ica |
Chala-Atico |
Tacna-Tarata |
Mollendo-Camaná |
|
Maca-Sallalli |
0.0548 |
0.0814 |
0.0925 |
0.0622 |
0.0730 |
|
Pisco-Ica |
0.0626 |
0.1274 |
0.0888 |
0.0466 |
0.0684 |
|
Chala-Atico |
0.0267 |
0.0924 |
0.1093 |
0.1078 |
0.0801 |
|
Tacna-Tarata |
0.0968 |
0.0995 |
0.0918 |
0.0336 |
0.0489 |
|
Mollendo-Camaná |
0.0592 |
0.1021 |
0.1643 |
0.0562 |
0.0693 |
Fuente: Elaboración propia. Datos IGP.
Tabla 8 Cálculo de Q3 para t = 3 meses
|
Estados |
Maca-Sallalli |
Pisco-Ica |
Chala-Atico |
Tacna-Tarata |
Mollendo-Camaná |
|
Maca-Sallalli |
0.1072 |
0.2063 |
0.1782 |
0.1087 |
0.1036 |
|
Pisco-Ica |
0.1462 |
0.2329 |
0.1629 |
0.1419 |
0.1421 |
|
Chala-Atico |
0.0935 |
0.1702 |
0.2025 |
0.1820 |
0.1534 |
|
Tacna-Tarata |
0.1540 |
0.2196 |
0.1793 |
0.0914 |
0.1088 |
|
Mollendo-Camaná |
0.1202 |
0.1716 |
0.2551 |
0.1227 |
0.1087 |
Fuente: Elaboración propia. Datos IGP.
Tabla 9 Cálculo de H1 para t = 1 mes
|
Estados |
Maca-Sallalli |
Pisco-Ica |
Chala-Atico |
Tacna-Tarata |
Mollendo-Camaná |
|
Maca-Sallalli |
0.3640 |
0 |
0 |
0 |
0 |
|
Pisco-Ica |
0 |
0.3939 |
0 |
0 |
0 |
|
Chala-Atico |
0 |
0 |
0.4163 |
0 |
0 |
|
Tacna-Tarata |
0 |
0 |
0 |
0.3705 |
0 |
|
Mollendo-Camaná |
0 |
0 |
0 |
0 |
0.4511 |
Fuente: Elaboración propia. Datos IGP.
Tabla 10 Cálculo de H3 para t = 3 meses
|
Estados |
Maca-Sallalli |
Pisco-Ica |
Chala-Atico |
Tacna-Tarata |
Mollendo-Camaná |
|
Maca-Sallalli |
0.7039 |
0 |
0 |
0 |
0 |
|
Pisco-Ica |
0 |
0.8260 |
0 |
0 |
0 |
|
Chala-Atico |
0 |
0 |
0.8015 |
0 |
0 |
|
Tacna-Tarata |
0 |
0 |
0 |
0.7530 |
0 |
|
Mollendo-Camaná |
0 |
0 |
0 |
0 |
0.7783 |
Fuente: Elaboración propia. Datos IGP.
3.4 APLICACIÓN DEL MODELO SEMI-MARKOV A LA MAGNITUD DE LOS SISMOS
Para aplicar el modelo semi-Markov a la magnitud de los sismos, se ha tenido en cuenta que el estudio está dirigido a sismos de gran magnitud, siendo así, se procedió a clasificar los sismos en tres intervalos: De magnitud 5.5 Mw a 5.99, de 6.00 Mw a 6.49 y de 6.50 a más. Estos intervalos constituyen los tres estados en el modelo semi-Márkov.
Para los cálculos se ha procedido de la misma manera como en el caso de las zonas geográficas.
El primer paso es hallar la matriz de transición.
Tabla 11 Matriz de transición para los estados de la magnitud de los sismos
|
Estados |
De 5.50 a 5.99 |
De 6.00 a 6.49 |
De 6.50 a mas |
|
De 5.50 a 5.99 |
0.7640 |
0.1880 |
0.0480 |
|
De 6.00 a 6.49 |
0.7830 |
0.1690 |
0.0480 |
|
De 6.50 a mas |
0.6250 |
0.2500 |
0.1250 |
Fuente: Elaboración propia. Datos IGP.
Figura 14 Distribución de Weibull para los tiempos de permanencia en la transición t11
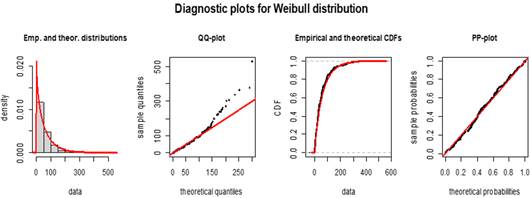
Fuente: Elaboración propia. Datos IGP.
Tabla 12 Parámetros de forma y escala de la distribución de los tiempos de espera para cada transición de la magnitud de los sismos
|
Transición |
P. Forma |
P. Escala |
Distribución |
|
t11 |
0.9147 |
60.3114 |
Weibull |
|
t12 |
1.0090 |
59.0916 |
Weibull |
|
t13 |
0.8589 |
64.0177 |
Weibull |
|
t21 |
0.9339 |
68.9664 |
Weibull |
|
t22 |
21.0433 |
7.9878 |
Cauchy |
|
t23 |
0.9220 |
70.7382 |
Weibull |
|
t31 |
0.9577 |
53.8768 |
Weibull |
|
t32 |
0.9485 |
29.2336 |
Weibull |
|
t33 |
0.6652 |
18.6559 |
Weibull |
Fuente: Elaboración propia. Datos IGP.
Y así, se procedió de la misma manera como en el caso de las zonas geográficas, llegamos al cálculo de H3, pata t = 3 meses:
Tabla 13 Cálculo de H3 para t = 3 meses
|
Estados |
De 5.50 a 5.99 |
De 6.00 a 6.49 |
De 6.50 a mas |
|
De 5.50 a 5.99 |
0.7660 |
0 |
0 |
|
De 6.00 a 6.49 |
0 |
0.7628 |
0 |
|
De 6.50 a mas |
0 |
0 |
0.8572 |
Fuente: Elaboración propia. Datos IGP.
3.5 APLICACIÓN DEL MODELO SEMI-MARKOV A LA PROFUNDIDAD DE LOS SISMOS
Definición de los estados de la profundidad:
Estado 1: Hasta 60 Km, Estado 2: De 60 a 100 Km, Estado 3: Mas de 100 Km
Tabla 14 Matriz de transición de los estados de la profundidad
|
Estados |
hasta 60Km |
De 60 a 100Km |
Más de 100Km |
|
hasta 60Km |
0.544 |
0.199 |
0.257 |
|
De 60 a 100Km |
0.536 |
0.167 |
0.298 |
|
Más de 100Km |
0.556 |
0.188 |
0.256 |
Fuente: Elaboración propia. Datos IGP.
Figura 15 Distribución de Weibull para los tiempos de permanencia en la transición t11
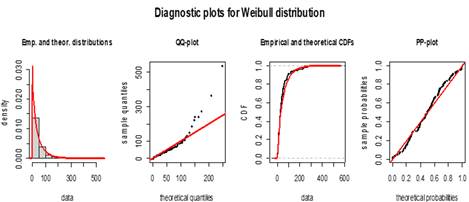
Fuente: Elaboración propia. Datos IGP.
Tabla 15 Parámetros de forma y escala de las distribuciones de los tiempos de espera en los estados de la profundidad
|
Transiciones |
P. Forma |
P. Escala |
|
Distribución |
|
t11 |
0.8851 |
47.2165 |
|
Weibull |
|
t12 |
0.8164 |
47.6679 |
|
Weibull |
|
t13 |
1.2009 |
68.4277 |
|
Weibull |
|
t21 |
0.8953 |
44.6217 |
|
Weibull |
|
t22 |
1.1513 |
116.2301 |
|
Weibull |
|
t23 |
1.2728 |
71.7330 |
|
Weibull |
|
t31 |
0.9337 |
68.4589 |
|
Weibull |
|
t32 |
0.9294 |
94.0653 |
|
Weibull |
|
t33 |
0.9615 |
75.6627 |
|
Weibull |
Fuente: Elaboración propia. Datos IGP.
En forma similar al caso de las zonas geográficas, la aplicación del modelo semi-Márkov a los estados de la profundidad, llegamos a calcular H3, para t = 3 meses.
Tabla 26 Cálculo de H3 para t = 3 meses
|
Estados |
hasta 60Km |
De 60 a 100Km |
Más de 100Km |
|
hasta 60Km |
0.8062 |
0 |
0 |
|
De 60 a 100Km |
0 |
0.7610 |
0 |
|
Más de 100Km |
0 |
0 |
0.6966 |
Fuente: Elaboración propia. Datos IGP.
4. DISCUSIÓN
Se han identificado 5 zonas geográficas con mayor frecuencia de sismos de magnitud mayor a 3.0 Mw, para lo cual se ha usado la herramienta estadística Cluster Análisis. Las zonas identificadas son: Zona 1: Maca-Sallalli; Zona 2: Pisco-Ica; Zona 3: Chala-Atico; Zona 4: Tacna-Tarata y Zona 5: Mollendo-Camaná.
De acuerdo con la metodología del modelo semi-Márkov, que se basa en la matriz de transición de los estados o zonas geográficas y en la matriz Hi (para i=1,3,6), que representa las probabilidades de ocurrencia de sismos en dichas zonas, podemos afirmar que las zonas geográficas segunda (Pisco-Ica) y tercera (Chala-Atico) presentan los mayores riesgos de ocurrencia de sismos de gran magnitud, con probabilidades de 0.82 y 0.80, respectivamente, en un periodo de 3 meses (ver Tabla 10, Cálculo de H3 para t = 3 meses para los estados de las zonas geográficas).
Para el caso de ocurrencia de sismos en las magnitudes (estados), podemos afirmar que es el tercer intervalo, el que presenta la mayor probabilidad de ocurrencia, con 0.85, lo cual nos indica que hay una mayor probabilidad que ocurra un sismo con mayor magnitud a 6.5Mw, en un periodo de 3 meses.
Para el caso de los estados de la profundidad, el resultado ha sido en el primer estado (hasta 60 Km), con la mayor probabilidad de 0.80, en sismos catalogados como superficiales, lo cual también es preocupante, dado que estos sismos son los más destructivos.
Se tomó en cuenta la afirmación teórica de (Sadegian, 2012) que “Las probabilidades de transición desde zonas geográficas a otras zonas geográficas, son independientes de las probabilidades de transición desde las magnitudes a otras magnitudes”. En el presente trabajo se extiende esta idea a la independencia de las probabilidades de transición desde los estados de la profundidad a otros estados de la profundidad.
Combinando los resultados de las tres dimensiones (Zonas geográficas, Magnitud y Profundidad) para sismos de alta magnitud (Magnitud mayor a 6.5 Mw), resultó para Pisco-Ica la probabilidad de ocurrencia de 0.826 * 0.8572 = 0.71 y para Chala-Atico, 0.8015 * 0.8572 = 0.70 en un periodo de 3 meses.
Si, además, en el periodo de 3 meses, consideramos a la profundidad superficial (profundidad hasta 60 Km) resultaría 0.8062 * 0.71 = 0.5724 y 0.8062* 0.70 = 0.5643 las probabilidades de ocurrencia de sismos de alta magnitud y superficiales; y en las zonas de mayor riesgo, esto es, para Pisco-Ica y para Chala-Atico respectivamente.
Entre las limitaciones al presente trabajo, se considera el ámbito de estudio, el cual abarca la región sur del Perú, el cual podría ser muy amplio. Si el modelo es aplicado a zonas de menor ámbito, los resultados podrían ser más precisos.
5. CONCLUSIONES
· Se ha identificado 5 zonas de mayor concentración de sismos en el sur del Perú, Zona 1: Maca-Sallalli;
Zona 2: Pisco-Ica;
Zona 3: Chala-Atico;
Zona 4: Tacna-Tarata y
Zona 5: Mollendo-Camaná.
· Con la aplicación del modelo semi-Márkov, a las zonas geográficas de mayor concentración de sismos del sur del Perú, se ha identificado la Zona 2 (Pisco-Ica) con probabilidad 0.82, pronóstico en un periodo de tiempo de 3 meses (ver Tabla 10, Cálculo de H3 para t = 3 meses para los estados de las zonas geográficas).
3. Para el caso de ocurrencia de sismos en las magnitudes (por estados), se afirma que es el tercer estado, la que presenta la mayor probabilidad de ocurrencia, con 0.85, lo cual nos indica que hay una alta probabilidad que ocurra un sismo con magnitud mayor a 6.5, en un periodo de 3 meses, (Ver Tabla 13 Cálculo de H3 para t = 3 meses).
4. También se ha aplicado el modelo semi-Márkov a los estados de la profundidad, resultando el primer estado (Profundidad hasta 60Km, sismos superficiales) con 0.8062, la mayor probabilidad de ocurrencia, (Ver Tabla 26 Cálculo de H3 para t = 3 meses).
5. Combinando los resultados anteriores, para sismos de alta magnitud (Magnitud > 6.5), resulta para la Zona 2 (Pisco-Ica) una probabilidad de ocurrencia de 0.71, pronóstico en un periodo de tiempo de 3 meses.
6. Si además consideramos a los sismos con profundidad superficial (Profundidad < 60 Km), para la Zona 2 (Pisco-Ica) la zona geográfica con mayor riesgo, y alta magnitud, resultó una probabilidad de ocurrencia de 0.57, pronóstico en un periodo de tiempo de 3 meses.
REFERENCIAS
Altinok, Y., & Kolcak, D. (1999). An application of the semi-Markov model for earthquake occurrences in North Anatolia, Turkey. Journal of the Balkan Geophysical Society, 2(4), 90-99.
https://www.balkangeophysoc.gr/online-journal/1999_V2/nov1999/pdf/v2-4-1.pdf
Alvarez, E. E. (2005). Alvarez, Estimation in stationary Markov renewal processes, with application to earthquake forecasting in Turkey. Environmental Science, Engineering, Mathematics Methodology and Computing in Applied Probability, 7, 119-130. https://doi.org/10.1007/s11009-005-6658-2
Garavaglia, E., & Pavani, R. (2011). About earthquake forecasting by Markov renewal processes. Methodology and Computing in Applied Probability, 13, 155-169.
https://doi.org/10.1007/s11009-009-9137-3
IGP, I. G. (2023). Descargar Datos. Instituto Geofísico del Perú.
Obtenido de https://ultimosismo.igp.gob.pe/descargar-datos-sismicos
Janssen, J., & Manca, R. (2006). Applied semi-Markov processes. Springer Science & Business Media. https://doi.org/10.1007/0-387-29548-8
Leonard Kaufman, Peter J. Rouseeuw (2005) Finding Groups in Data. An Introduction to Cluster Analysis. Wiley-Interscience
Masala, G. (2012). Earthquakes occurrences estimation through a parametric semi-Markov approach. Journal of Applied Statistics, 39(1), 81-96.
https://doi.org/10.1080/02664763.2011.578617
Sadeghian, R. (2012). Forecasting time and place of earthquakes using a Semi-Markov model (with case study in Tehran province). Journal of Industrial Engineering International, 8, 1-7. https://doi.org/10.1186/2251-712X-8-20
Tavera, H. (2001). Peligro sísmico en Lima y el país. Revista del Centro de Estudios y Prevención de desastres, 8(14), 30-35. http://hdl.handle.net/20.500.12816/832
Tavera, H., Salas, H., Jimenez, C., Antayhua Vera, Y. T., Vilcapoma, L., Millones, J., ... & Rodríguez, S. (2001). El terremoto de la región del sur del Perú del 23 de junio de 2001. Instituto Geofísico del Perú. http://hdl.handle.net/20.500.12816/1121
Tavera, H., Bernal, I., & Salas, H. (2007). El sismo de Pisco del 15 de agosto, 2007 (7.9 Mw) departamento de Ica - Perú (informe preliminar). Instituto Geofísico del Perú. http://hdl.handle.net/20.500.12816/1115