Revista IECOS, 24(2), 25-58
ESTIMACIONES DE MERCADO DE LA TASA DE INTERES REAL NATURAL: EVIDENCIA DE LOS MERCADOS DE BONOS LATINOAMERICANOS
MARKET-BASED ESTIMATES OF THE NATURAL REAL RATE: EVIDENCE FROM LATIN AMERICAN BOND MARKETS
Luis
Ceballos![]() 1, Jens
H. E. Christensen
1, Jens
H. E. Christensen![]() 2, Damian
Romero
2, Damian
Romero![]() 3
3
1University of San Diego, San Diego, Estados Unidos
2Federal Reserve Bank of San Francisco, San Francisco, Estados Unidos
3Central Bank of Chile, Santiago, Chile
E-mail: 1luisceballos@sandiego.edu, 2jens.christensen@sf.frb.org, 3dromeroc@bcentral.cl
1https://orcid.org/0000-0002-8287-3782, 2https://orcid.org/0000-0001-7494-2736, 3https://orcid.org/0000-0002-0139-3454
https://doi.org/10.21754/iecos.v24i2.2042
Recibido (Received): 15/12/2023 Aceptado (Accepted): 17/12/2023 Publicado (Published): 31/12/2023
RESUMEN
Proporcionamos estimaciones basadas en el mercado de bonos para la tasa real natural, es decir, la tasa de interés real a corto plazo en estado estacionario, para Brasil, Chile y México. Nuestro enfoque utiliza un modelo financiero dinámico de la estructura de tasas de interés estimado directamente sobre los precios de los bonos individuales indexados a la inflación ajustados por premios por liquidez específicos de los bonos y premios por plazo. En primer lugar, observamos que premios por liquidez de los bonos indexados a la inflación en los tres países son considerables y varían significativamente. En segundo lugar, observamos grandes diferencias en sus tasas de interés reales de equilibrio: la de Brasil es alta y volátil, la de México estable pero elevada, mientras que la de Chile es baja y ha caído de forma persistente. Aunque inciertas, nuestras estimaciones tienen importantes implicancias para la conducción de la política monetaria en estos tres países.
Palabras clave: modelo de estructura temporal libre de arbitraje afín, fricciones en el mercado financiero, política monetaria, rstar
ABSTRACT
For Brazil, Chile, and Mexico, we offer market-based estimates of the natural real rate, or the steady-state short-term real interest rate. Our methodology makes use of a dynamic term structure finance model that is directly estimated from the prices of individual inflation-indexed bonds, adjusting for real term premia and bond-specific liquidity. First, we discover that there is substantial heterogeneity in the inflation-indexed bond liquidity premia across all three nations. Second, we discover significant variations in their projected equilibrium real rates: Chile's is low and has been declining steadily, Mexico's is constant but high, and Brazil's is huge and erratic. Our estimates, albeit imprecise, may have significant effects on how monetary policy is implemented in these three nations.
JEL Classification: C32, E43, E52, G12
Keywords: affine arbitrage-free term structure model, financial market frictions, monetary policy, rstar
1. INTRODUCCIÓN
Una idea fundamental y ampliamente reconocida en economía es la tasa real de equilibrio. Para los inversores, los pronósticos de las tasas de descuento futuras utilizadas para valorar los activos están ancladas en el nivel de equilibrio de la tasa real a corto plazo (ver, por ejemplo, Clarida, 2014). El nivel de equilibrio, también conocido como tasa de interés natural, sirve de patrón neutro para que investigadores y bancos centrales calibren la orientación de la política monetaria: Si la tasa de interés real a corto plazo es superior a la tasa natural, la política monetaria es contractiva; si es inferior, es expansiva. Para poner en práctica directrices de política monetaria bien conocidas, como la regla de Taylor, también se necesita una estimación fiable de la tasa real de equilibrio. [1]
Mientras que la mayoría de las estimaciones existentes de esta variable económica clave se extraen de modelos y datos macroeconómicos, en este artículo seguimos a Christensen y Rudebusch (2019, en adelante CR) y utilizamos modelos financieros. Específicamente, nos basamos en los precios de los bonos indexados a la inflación de tres países latinoamericanos para nuestro análisis, Brasil, Chile y México, y, por lo tanto, ofrecemos una perspectiva única de los mercados emergentes sobre las tendencias recientes de la tasa real natural. [2]
Estos activos compensan a los inversores por la pérdida de poder adquisitivo resultante de la inflación de los precios internos, ya que sus pagos de cupón y principal están vinculados al índice de precios al consumidor (IPC) de cada país. [3] En consecuencia, sus precios reflejan directamente los rendimientos reales. La premisa básica de nuestro análisis es que la visión de los participantes en los mercados financieros sobre el estado estacionario de cada economía, incluido su tasa de interés natural, se reflejan en las expectativas a más largo plazo codificadas en los precios de los bonos.
Los datos sobre bonos también ofrecen ventajas adicionales. En primer lugar, los tres países tienen mercados bastante líquidos de deuda pública indexada a la inflación. En segundo lugar, con vencimientos de hasta 40 años en el caso de Brasil, estos mercados de bonos indexados a la inflación contienen información prospectiva y, por lo tanto, proporcionan evidencia acerca de las tasas de equilibrio de largo plazo.
En tercer lugar, al basarnos en bonos indexados a la inflación, evitamos cualquier problema relacionado con el límite inferior cero (zero lower bound) que pueda aplicarse a las tasas cortas y a otras tasas de interés nominales. Además, dado que los factores subyacentes que afectan a las tasas de interés a largo plazo son probablemente de naturaleza global—como los cambios demográficos mundiales, los cambios en las tendencias de productividad o los ajustes persistentes en las cadenas de suministro globales en el mundo post pandemia—estos tres mercados de deuda pública pueden ser tan informativos como cualquier otro mercado emergente de deuda soberana. Así pues, consideramos que los datos de bonos de estos tres países son representativos de los mercados de bonos emergentes en general.
A pesar de estas ventajas, existen ciertas dificultades empíricas a la hora de utilizar bonos indexados a la inflación para calcular la tasa de interés real a corto plazo en estado estacionario. Uno de los problemas es que el precio de los bonos indexados a la inflación incluye un premio por plazo real. Lo más probable es que el premio sea positivo porque las curvas de rendimiento de los bonos indexados a la inflación en nuestros datos tienen una pendiente positiva. Sin embargo, no se sabe con certeza nada sobre su tamaño o variabilidad. Además, Cardozo y Christensen (2023) sostienen que, incluso con una cantidad nocional relativamente alta de bonos indexados a la inflación en circulación en los tres países considerados, estos activos conllevan naturalmente un nivel significativo de riesgo de liquidez por motivos estructurales. En primer lugar, dado que proporcionan una cobertura frente al riesgo de inflación, es probable que se transen menos que los bonos nominales. En segundo lugar, como este argumento de cobertura sólo se aplica a los inversionistas nacionales cuyos gastos de consumo siguen el IPC local, los inversionistas extranjeros no se beneficiarán de la tenencia de estos valores. En consecuencia, las transacciones de bonos indexados a la inflación acaban concentrándose entre inversores nacionales pacientes que compran y mantienen en su portafolio, como los fondos de pensiones y las compañías de seguros (buy and hold). Es razonable suponer que los inversores requieren un premio a cambio de asumir el riesgo de liquidez que conlleva la tenencia de bonos indexados a la inflación, pero se necesita más investigación para determinar el tamaño y la variabilidad temporal de este premio. Por último, es importante señalar que realizamos nuestro análisis bajo el supuesto estándar de que los bonos soberanos están libres de impago. Por lo tanto, no consideramos el riesgo de crédito. Aunque esta omisión puede sesgar en cierta medida nuestros resultados, en apoyo de esta elección de modelo, señalamos que el ratio deuda pública/PIB nominal en 2022 era del 72,9%, 37,6% y 48,3% para Brasil, Chile y México, respectivamente, [4] que son valores bajos en comparación con la mayoría de las economías avanzadas, incluido Estados Unidos.
En base a lo anterior, utilizamos un modelo dinámico libre de arbitraje para los rendimientos reales aumentado con un factor de riesgo de liquidez para estimar la tasa de interés natural en presencia de premios por plazo reales y de liquidez. El factor de riesgo de liquidez puede identificarse en función de su efecto específico para cada activo, como muestra Andreasen, Christensen y Riddell (2021, en adelante ACR). En lugar de utilizar los rendimientos de curvas sintéticas ajustadas, nuestra estrategia emplea los precios de bonos reales efectivamente transados en el mercado.
La idea fundamental es que a través del tiempo una fracción cada vez mayor del monto en circulación acabará en el portafolio de inversionistas buy and hold. Este efecto sugiere que, dado el comportamiento prospectivo de los inversores, la vulnerabilidad de un bono al factor de liquidez de todo el mercado diferirá en función de su proximidad al vencimiento. Mediante el análisis de corte transversal de precios de bonos a lo largo del tiempo, cada uno con un único plazo de vencimiento y tiempo desde la emisión, podemos determinar el factor de liquidez global, así como el grado en que cada bono se ve afectado por él. En los primeros años de nuestras muestras, cuando sólo se dispone de un pequeño número de bonos, esta técnica es especialmente útil para evaluar la deuda indexada a la inflación.[5]
La formulación teórica del modelo libre de arbitraje también identifica un premio por plazo real variable en el tiempo para los precios de los bonos indexados a la inflación. Al determinar el premio por liquidez y el premio por plazo, podemos estimar la estructura temporal subyacente de tasa reales sin fricciones y la tasa de interés real natural, que caracterizamos como la tasa real de corto plazo promedio proyectada a lo largo de un período de cinco años que comienza con cinco años de antelación, como en CR.
Nuestros resultados se resumen a continuación. En primer lugar, en línea con el razonamiento presentado en Cardozo y Christensen (2023), existen premios por riesgo de liquidez significativos y variables en el tiempo en los tres mercados. Esto subraya la importancia de tener en cuenta estos premios en nuestro análisis. En segundo lugar, existe una variación significativa en las estimaciones de la tasa real natural entre las tres economías consideradas, reflejando las diferencias en sus fundamentos. Dejamos para análisis futuro la comprobación de si esto es cierto para otras economías en desarrollo de América Latina y de otros lugares. Como ejercicio final, utilizamos nuestras estimaciones de la tasa real natural para construir una medida de la orientación de la política monetaria en cada país. Estas medidas sugieren que, aunque acomodaticia durante el periodo de la pandemia, la política monetaria alcanzó una orientación más restrictiva en los tres países al final del periodo de la muestra. Sin embargo, subrayamos que nuestras estimaciones de la tasa real natural están asociadas a una incertidumbre significativa, que merece la pena tener en cuenta si se utilizan para extraer implicaciones para la conducción de la política monetaria.
El resto del artículo se estructura del siguiente modo. En la sección 2 se describen los datos sobre bonos indexados a la inflación, y en la sección 3 se presentan los resultados empíricos y los modelos de estructura de tasas libre de arbitraje. La estimación de premios por liquidez se examina en la sección 4, y nuestras estimaciones de la tasa real natural basadas en bonos se analizan en la sección 5. La sección 6 concluye. Nuestros datos brasileños se detallan en el apéndice junto con un resumen del proceso de selección de modelos de cada país.
2. LOS DATOS DE LOS BONOS INDEXADOS A LA INFLACIÓN
En esta sección, describimos brevemente los datos de los bonos indexados a la inflación que utilizamos en las estimaciones de nuestro modelo.
Nuestra muestra de bonos brasileños indexados a la inflación fue descargada desde Bloomberg y contiene los precios de 31 bonos desde noviembre de 2005 hasta septiembre de 2023. El Apéndice A proporciona más detalles sobre nuestra muestra de bonos brasileños.[6]
El gobierno chileno emitió sus primeros bonos indexados a la inflación en la década de 1960. Estos bonos se conocen como bonos tesorería UF (BTU) y bonos del Banco Central en UF (BCU). Nuestra muestra se obtuvo de Riskamerica (www.riskamerica.com), abarcando el periodo comprendido entre agosto de 2003 y julio de 2023, y contiene los precios de un total de 72 bonos. Fue analizada por primera vez en Ceballos et al. (2024). Por lo tanto, remitimos a los lectores interesados a ese documento para más detalles sobre los datos chilenos. [7]
Los bonos mexicanos indexados a la inflación se conocen como udibonos. Nuestra muestra de precios de udibonos fue descargada de Bloomberg y cubre el periodo de mayo de 2009 a septiembre de 2023 con precios para un total de 20 bonos, muestra que fue analizada por primera vez por Beauregard et al. (2021). Por lo tanto, remitimos a los lectores interesados a ese documento para obtener detalles adicionales sobre nuestros datos mexicanos.
Fundamentalmente, debido al desfase de indexación en sus pagos, los precios de los bonos indexados a la inflación próximos a su vencimiento tienden a ser bastante impredecibles, como mencionan Gürkaynak et al. (2010) y ACR. En consecuencia, excluimos los bonos indexados a la inflación de cada una de las tres muestras en el momento en que les queda menos de un año para su vencimiento, con el fin de facilitar la estimación del modelo.
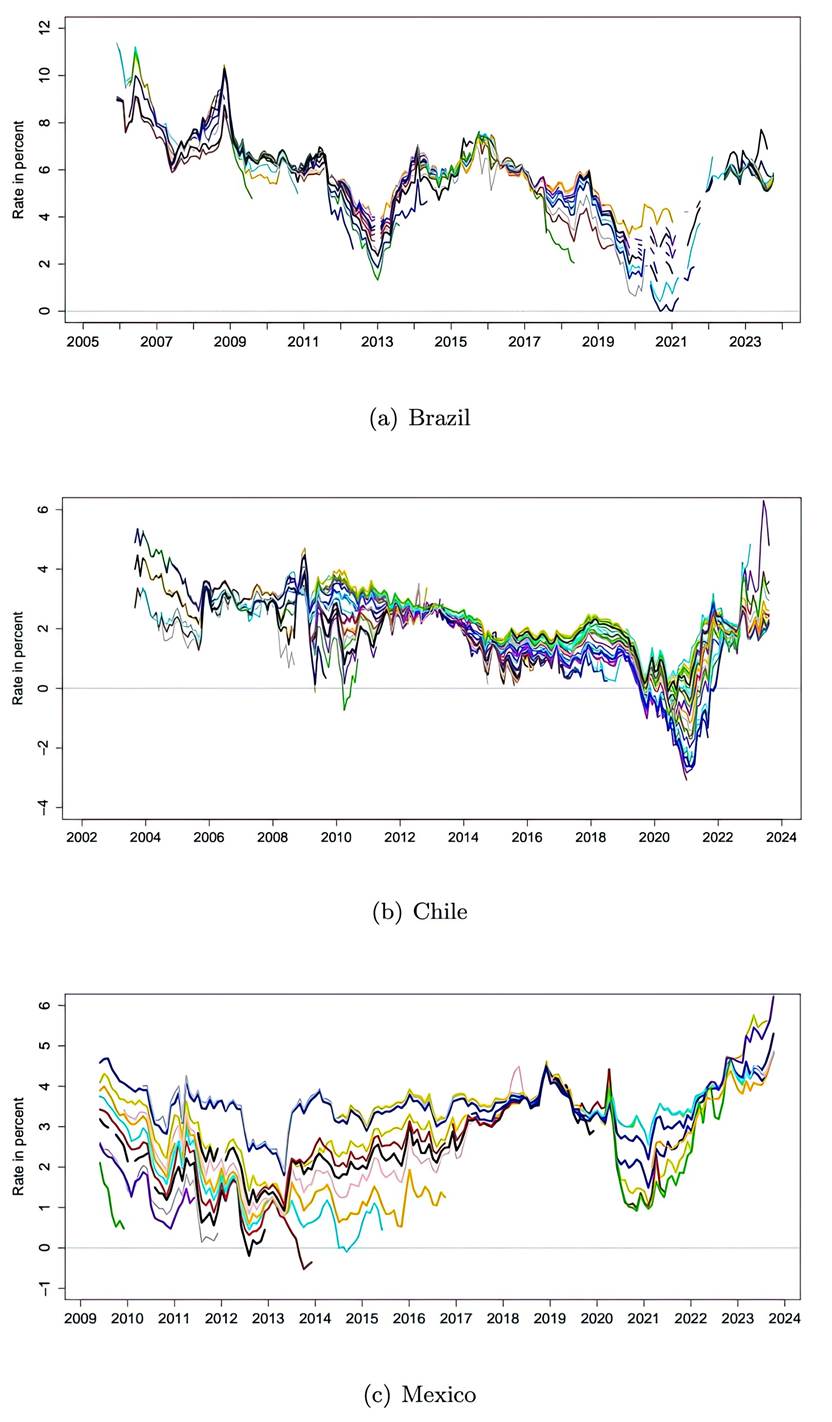
El gráfico 1 muestra las series de rendimiento al vencimiento (Yield to Maturity) de todos los bonos indexados a la inflación de nuestra muestra para cada uno de los tres países. Las tres muestras de rendimientos se caracterizan por una pronunciada variación del ciclo económico. Además, los rendimientos reales en los tres países cayeron bruscamente en el punto álgido de la pandemia. Fuera de ese período, los rendimientos se mantuvieron estables. Además, en general operan a niveles diferentes, con Brasil ofreciendo las tasas reales más altas, mientras que Chile tiende a tener las tasas reales más bajas seguido de cerca por México. [8]
Un aspecto clave a tener en cuenta es que tanto el número de bonos como su distribución de vencimientos varían en las tres muestras. Por lo tanto, estos rendimientos no son directamente comparables. Afortunadamente, nuestros modelos de estructura temporal nos permiten tener en cuenta con precisión estas diferencias en las muestras, además de proporcionar ajustes a las tasas reales observadas tanto para los premios por riesgo de liquidez específicas de los bonos como para los premios temporales generales. De este modo, obtenemos información sobre las expectativas de los inversionistas respecto a las tasas reales a corto plazos subyacentes en cada uno de estos tres importantes mercados de bonos indexados a la inflación. El resto de este documento está dedicado a esta tarea.
Figura 1
Rendimiento al vencimiento de bonos indexados a la inflación
3. ESTIMACIÓN DEL MODELO Y RESULTADOS
Lo primero que tratamos en esta sección es cómo modelamos los rendimientos en un escenario en el que no existen fricciones de liquidez. A continuación, describimos en detalle el modelo actualizado que explica premios por liquidez de las tasas de los bonos indexados a la inflación. Luego, se describen las limitaciones establecidas para llevar a cabo la identificación y estimación econométrica de este modelo. Concluimos la sección con una breve explicación de nuestro proceso de selección de modelos y de los resultados de las estimaciones correspondientes.
3.1. UN MODELO DE RENDIMIENTOS REALES SIN ARBITRAJE Y SIN FRICCIONES
Nos concentramos en el modelo de estructura temporal dinámica afín presentado en Christensen et al. (2011) para representar las variables sin fricciones que determinan cada curva de rendimiento real. [9]
En
este modelo Nelson-Siegel libre de arbitraje (AFNS), el vector de estado se
denota por ![]() donde
donde ![]() es un factor de nivel,
es un factor de nivel, ![]() es un factor de pendiente
y
es un factor de pendiente
y ![]() es un factor de
curvatura. La tasa real instantánea libre riesgo se define como
es un factor de
curvatura. La tasa real instantánea libre riesgo se define como
![]()
Las siguientes ecuaciones diferenciales estocásticas proporcionan la dinámica neutral al riesgo (o ℚ) de las variables de estado[10]
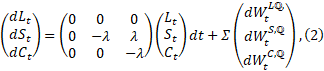
donde Σ es la matriz de covarianza constante, a menudo conocida como volatilidad. La estructura de carga factorial de Nelson-Siegel es preservada por los rendimientos de bonos reales de cero cupón basados en esta formulación de la dinámica bajo ℚ como
![]()
donde
![]() es
un término de convexidad que garantiza que no haya arbitraje ajustando la forma
funcional de Nelson y Siegel (1987) (véase Christensen et al., 2011).
es
un término de convexidad que garantiza que no haya arbitraje ajustando la forma
funcional de Nelson y Siegel (1987) (véase Christensen et al., 2011).
Definimos
los premios por riesgo que vinculan la dinámica de estos factores bajo la medida
ℚ con la dinámica bajo la medida ℙ del mundo real (o físico) para
terminar la descripción del modelo y llevarlo a la práctica empírica. Cabe
destacar que, aparte del requisito de volatilidad constante, los componentes
dinámicos no están restringidos bajo la medida ℚ de manera empírica.
Empleamos la definición de premio por riesgo esencialmente afín presentada por
primera vez por Duffee (2002) para permitir la aplicación empírica. Esta
especificación sugiere que los premios por riesgo ![]() en
el marco gaussiano dependen de las variables de estado; es decir, cuando
en
el marco gaussiano dependen de las variables de estado; es decir, cuando ![]() ∈
∈ ![]() y
y
![]() ∈
∈ ![]() contienen
parámetros no restringidos,
contienen
parámetros no restringidos, ![]() adopta
la forma
adopta
la forma
![]()
En consecuencia, la dinámica bajo ℙ para el modelo AFNS de tres factores sin restricciones resultante viene dada por
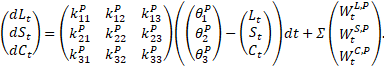
En la estimación del filtro de Kalman, ésta es la ecuación de transición.
3.2. UN MODELO DE RENDIMIENTOS REALES SIN ARBITRAJE CON RIESGO DE LIQUIDEZ
Para
tener en cuenta los premios por liquidez de los precios de los bonos indexados
a la inflación que utilizamos en la investigación empírica, modificamos el
modelo sin fricciones que se introdujo anteriormente. Para ello, utilizaremos
el modelo AFNS-L para denotar el modelo de cuatro factores con ajuste del
premio por riesgo de liquidez y dejaremos que ![]() represente
su vector de estado. La tasa real instantánea libre de riesgo y sin fricciones se
define mediante la ecuación (1), que es la misma que en el modelo no aumentado.
Por otra parte, la dinámica neutral al riesgo de las variables de estado
necesarias para la fijación de precios viene dada por
represente
su vector de estado. La tasa real instantánea libre de riesgo y sin fricciones se
define mediante la ecuación (1), que es la misma que en el modelo no aumentado.
Por otra parte, la dinámica neutral al riesgo de las variables de estado
necesarias para la fijación de precios viene dada por
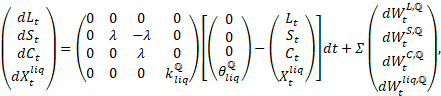
donde la matriz de volatilidad Σ sigue siendo diagonal.
En el modelo AFNS-L aumentado, los rendimientos de los bonos indexados a la inflación son sensibles al riesgo de liquidez específico de los bonos porque su fijación de precios se realiza utilizando una función de descuento que tiene en cuenta el riesgo de liquidez propio de cada bono en lugar de la función de descuento real sin fricción:
![]()
La siguiente forma exponencial-afín
representa entonces el valor actual neto de una sola unidad de consumo pagada
por el bono i en el momento ![]() , según CR:
, según CR:
![]()
![]()
Esta
conclusión demuestra que el modelo pertenece a la clase de modelos de
estructura temporal afín gaussiana. Obsérvese que el modelo AFNS puede
restablecerse garantizando que ![]() para
cada
para
cada ![]() .
.
Consideremos
un bono i, que se emitió en el
momento ![]() , tiene
una fecha de vencimiento de
, tiene
una fecha de vencimiento de ![]() , y paga un cupón anual
, y paga un cupón anual ![]() semestralmente.
Su costo, que es igual a su valor actual neto, viene determinado por[11]
semestralmente.
Su costo, que es igual a su valor actual neto, viene determinado por[11]
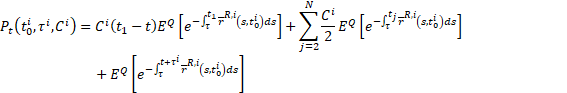
Los bonos indexados a la inflación de los tres mercados tienen el indicado anteriormente porque carecen de una opción de protección contra la deflación incorporada, a diferencia de los valores del Tesoro estadounidense protegidos contra la inflación (TIPS). La fórmula de fijación de precios de los bonos que utilizamos sólo tiene una pequeña omisión. No se tiene en cuenta el desfase en la indexación a la inflación del bono. Dado que eliminamos los bonos de nuestra muestra cuando les queda menos de un año para su vencimiento, el posible error derivado de esta omisión debería ser mínimo (véase Grishchenko y Huang, 2013).
Por
último, definimos una estructura de premios por riesgo esencialmente afín una
vez más para terminar la descripción del modelo AFNS-L. Esto permite que los
premios ![]() tengan la siguiente forma
afín general
tengan la siguiente forma
afín general
![]()
donde
los parámetros no restringidos están contenidos en ![]() ∈
∈ ![]() y
y
![]() ∈
∈ ![]() . En consecuencia, la dinámica
bajo ℙ para el modelo AFNS-L de cuatro factores sin restricciones
resultante viene dada por
. En consecuencia, la dinámica
bajo ℙ para el modelo AFNS-L de cuatro factores sin restricciones
resultante viene dada por
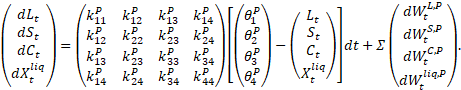
En la estimación del filtro de Kalman, ésta es la ecuación de transición.
3.3. ESTIMACIÓN DEL MODELO E IDENTIFICACIÓN ECONOMÉTRICA
Debido a la relación no lineal entre las variables de estado y los precios de los bonos, el modelo no puede estimarse utilizando el filtro de Kalman estándar. En su lugar, empleamos el filtro de Kalman ampliado, tal y como se describe en Kim y Singleton (2012); los detalles se recogen en CR. Además, escalamos los precios de los bonos en función de su duración para que los errores ajustados sean comparables entre bonos con diferentes vencimientos.
Como resultado, la ecuación de medida de los precios de los bonos tiene la siguiente forma
![]()
donde
![]() es
el precio implícito en el modelo del bono
es
el precio implícito en el modelo del bono ![]() ,
y
,
y ![]() es su duración, la cual
se determina antes de la estimación. Para ver evidencia a favor de esta
ecuación de medida, véase Andreasen et al. (2019).
es su duración, la cual
se determina antes de la estimación. Para ver evidencia a favor de esta
ecuación de medida, véase Andreasen et al. (2019).
Además,
sin imponer más estructura, no se puede determinar el grado del componente de
riesgo de liquidez porque es una característica latente que no se observas. Para
el mercado brasileño permitimos un factor unitario en este componente (es
decir, ![]() = 1)
para el primer bono a 40 años emitido el 15 de septiembre de 2004, con
vencimiento el 15 de mayo de 2045, con un cupón del 6 por ciento. Para el
mercado chileno usamos la estrategia empleada por Ceballos et al. (2024),
utilizando el primer bono a 20 años, que se emitió el 11 de septiembre de 2002
y con vencimiento el 1 de septiembre de 2022, con un cupón del 5 por ciento y
con un ponderador unitario en el factor de riesgo específico del bono. Finalmente,
para el mercado mexicano, seguimos a Beauregard et al. (2021) utilizando un
ponderador unitario para el factor de riesgo para el primer bono mexicano de
udibonos a 30 años, con fecha de emisión el 5 de enero de 2006 y vencimiento el
22 de noviembre de 2035.
= 1)
para el primer bono a 40 años emitido el 15 de septiembre de 2004, con
vencimiento el 15 de mayo de 2045, con un cupón del 6 por ciento. Para el
mercado chileno usamos la estrategia empleada por Ceballos et al. (2024),
utilizando el primer bono a 20 años, que se emitió el 11 de septiembre de 2002
y con vencimiento el 1 de septiembre de 2022, con un cupón del 5 por ciento y
con un ponderador unitario en el factor de riesgo específico del bono. Finalmente,
para el mercado mexicano, seguimos a Beauregard et al. (2021) utilizando un
ponderador unitario para el factor de riesgo para el primer bono mexicano de
udibonos a 30 años, con fecha de emisión el 5 de enero de 2006 y vencimiento el
22 de noviembre de 2035.
Por
último, observamos que puede resultar difícil determinar si los parámetros ![]() son
demasiado grandes o pequeños. Por lo tanto, seguimos a ACR e imponemos la
restricción de que se encuentren dentro del intervalo de 0,01 a 10. Para
garantizar la estabilidad numérica durante la optimización del modelo se añade la
restricción de que los parámetros
son
demasiado grandes o pequeños. Por lo tanto, seguimos a ACR e imponemos la
restricción de que se encuentren dentro del intervalo de 0,01 a 10. Para
garantizar la estabilidad numérica durante la optimización del modelo se añade la
restricción de que los parámetros ![]() deben
estar comprendidos entre 0 y 100, la cual no es una restricción que afecte en
el óptimo.
deben
estar comprendidos entre 0 y 100, la cual no es una restricción que afecte en
el óptimo.
3.4. SELECCIÓN DEL MODELO
La
definición de la matriz de reversión a la media ![]() es
crucial para el cálculo de la tasa real natural y los premios por plazo real
relacionadas, como se indica en Ceballos et al. (2024). Restringiendo a cero
el parámetro no diagonal menos importante de
es
crucial para el cálculo de la tasa real natural y los premios por plazo real
relacionadas, como se indica en Ceballos et al. (2024). Restringiendo a cero
el parámetro no diagonal menos importante de ![]() y
reestimando el modelo, utilizamos un enfoque de modelización de general a
específico para obtener la caracterización adecuada de la dinámica del mundo
real para cada modelo. Este proceso continúa hasta que se alcanza la
especificación más parsimoniosa, que tiene una matriz
y
reestimando el modelo, utilizamos un enfoque de modelización de general a
específico para obtener la caracterización adecuada de la dinámica del mundo
real para cada modelo. Este proceso continúa hasta que se alcanza la
especificación más parsimoniosa, que tiene una matriz ![]() diagonal.
Según Christensen et al. (2014), [12]
la selección de la especificación definitiva viene determinada por el valor del
criterio de información bayesiano (BIC). El apéndice B contiene los datos
resumidos del procedimiento de selección de modelos para cada nación.
diagonal.
Según Christensen et al. (2014), [12]
la selección de la especificación definitiva viene determinada por el valor del
criterio de información bayesiano (BIC). El apéndice B contiene los datos
resumidos del procedimiento de selección de modelos para cada nación.
La
especificación (10) minimiza el BIC para los datos de bonos brasileños, con una
matriz ![]() proporcionada
por
proporcionada
por
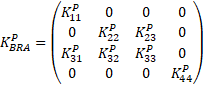 .
.
Los parámetros calculados del modelo brasileño recomendado se presentan en la siguiente tabla.
Tabla 1
Parámetros Dinámicos Estimados del Modelo AFNS-L Brasileño Preferido
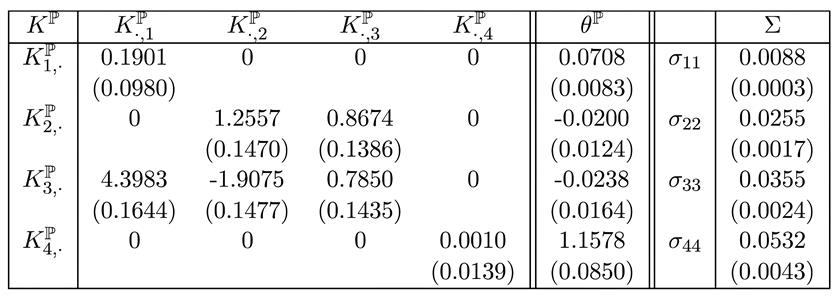
Nota.
La tabla presenta los parámetros estimados para la matriz diagonal Σ, el
vector ![]() y
la matriz
y
la matriz ![]() para
el modelo brasileño AFNS-L que se prefiere en función del BIC. λ se
proyecta en 0,3042 (0,0093),
para
el modelo brasileño AFNS-L que se prefiere en función del BIC. λ se
proyecta en 0,3042 (0,0093), ![]() en
2,7175 (0,0950) y
en
2,7175 (0,0950) y ![]() en 0,0167 (0,0010).
11.408,63 es el mayor valor de la probabilidad logarítmica. Las desviaciones
estándar de los parámetros calculados se indican con los valores entre
paréntesis.
en 0,0167 (0,0010).
11.408,63 es el mayor valor de la probabilidad logarítmica. Las desviaciones
estándar de los parámetros calculados se indican con los valores entre
paréntesis.
Para los datos chilenos, el BIC se minimiza mediante la especificación (10), que tiene una matriz de reversión de medias dada por
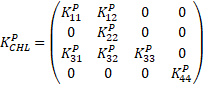 .
.
La Tabla 2 reporta los parámetros estimados de la especificación chilena recomendada, que son similares a los encontrados en Ceballos et al. (2024).
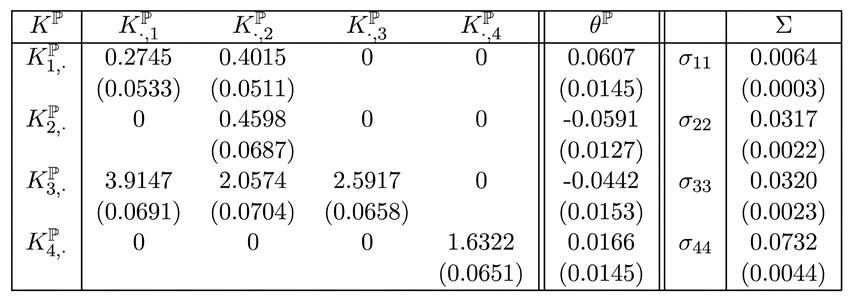
Tabla 2
Parámetros dinámicos estimados del modelo AFNS-L chileno preferido
Nota.
La matriz diagonal Σ, el vector ![]() y los parámetros de
estimación de la matriz
y los parámetros de
estimación de la matriz ![]() para
el modelo AFNS-L chileno seleccionado basado en el BIC se muestran en la tabla.
λ se proyecta en 0,3954 (0,0096),
para
el modelo AFNS-L chileno seleccionado basado en el BIC se muestran en la tabla.
λ se proyecta en 0,3954 (0,0096), ![]() en
3,2517 (0,0669) y
en
3,2517 (0,0669) y ![]() en
0,0096 (0,0004). El valor máximo es una probabilidad logarítmica de 36.579,89.
Las desviaciones estándar de los parámetros se estiman y se representan con los
números entre paréntesis.
en
0,0096 (0,0004). El valor máximo es una probabilidad logarítmica de 36.579,89.
Las desviaciones estándar de los parámetros se estiman y se representan con los
números entre paréntesis.
La
especificación (12) minimiza el BIC para los datos de bonos mexicanos, con una
matriz ![]() proporcionada por
proporcionada por
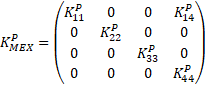 .
.
La tabla 3 presenta los parámetros estimados de la especificación mexicana seleccionada.
Tabla 3
Parámetros dinámicos estimados del modelo AFNS-L mexicano preferido
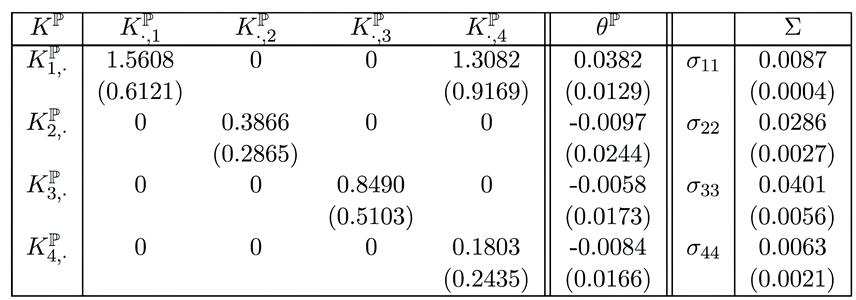
Nota.
Para el modelo AFNS-L mexicano favorecido, los parámetros estimados BIC de la
matriz ![]() , el vector
, el vector ![]() y la matriz diagonal
Σ se muestran en la tabla. Una estimación aproximada de λ es 0,8673
(0,0446),
y la matriz diagonal
Σ se muestran en la tabla. Una estimación aproximada de λ es 0,8673
(0,0446), ![]() es 0,0493 (0,0558) y
es 0,0493 (0,0558) y ![]() es
0,0400 (0,0362). El valor máximo de verosimilitud logarítmica alcanzado es
7.625,03. Las desviaciones estándar de los parámetros se estiman y se
representan con los números entre paréntesis.
es
0,0400 (0,0362). El valor máximo de verosimilitud logarítmica alcanzado es
7.625,03. Las desviaciones estándar de los parámetros se estiman y se
representan con los números entre paréntesis.
Estos
resultados proporcionan dos conclusiones. En primer lugar, los resultados de
los procedimientos de selección de modelos muestran que las curvas de
rendimiento real en los tres países considerados operan cada una de maneras
únicas, como se refleja en las diferentes matrices ![]() de reversión a la media
preferidas. En segundo lugar, debido a la naturaleza latente de nuestros
modelos, en general es difícil comparar los parámetros estimados. Sin embargo,
el parámetro λ puede interpretarse de forma significativa en todos los
modelos, ya que determina la tasa de decrecimiento de la carga asociada al
factor de la pendiente y la madurez en la que la carga del factor de curvatura
alcanza su punto máximo. Por lo tanto, su valor relativamente bajo para los
datos brasileños y chilenos implica que los modelos para estos dos países ponen
más énfasis en ajustar los precios de los bonos a largo plazo, mientras que el
modelo mexicano con un valor para λ que es más del doble del tamaño de los
de los otros dos modelos pone relativamente más énfasis en ajustar los precios
de los bonos a corto plazo.
de reversión a la media
preferidas. En segundo lugar, debido a la naturaleza latente de nuestros
modelos, en general es difícil comparar los parámetros estimados. Sin embargo,
el parámetro λ puede interpretarse de forma significativa en todos los
modelos, ya que determina la tasa de decrecimiento de la carga asociada al
factor de la pendiente y la madurez en la que la carga del factor de curvatura
alcanza su punto máximo. Por lo tanto, su valor relativamente bajo para los
datos brasileños y chilenos implica que los modelos para estos dos países ponen
más énfasis en ajustar los precios de los bonos a largo plazo, mientras que el
modelo mexicano con un valor para λ que es más del doble del tamaño de los
de los otros dos modelos pone relativamente más énfasis en ajustar los precios
de los bonos a corto plazo.
3.5. AJUSTE DEL MODELO
Por último, revisamos el ajuste del modelo. La tabla 4 evalúa hasta qué punto cada uno de nuestros tres modelos seleccionados se ajusta a los valores de mercado de los bonos con cupón de cada muestra. Para garantizar que los errores de fijación de precios son iguales en todos los valores, cabe señalar que se calculan utilizando el rendimiento implícito de cada bono con cupón. [13] En la tabla 4 se presenta un resumen de las estadísticas del ajuste a todos los bonos de cada muestra, divididos en tramos de vencimiento. También se indica cuántas observaciones hay en cada grupo de vencimientos del mercado.
Tabla 4
Resumen estadístico de los errores de ajuste de los rendimientos indexados de la deuda pública
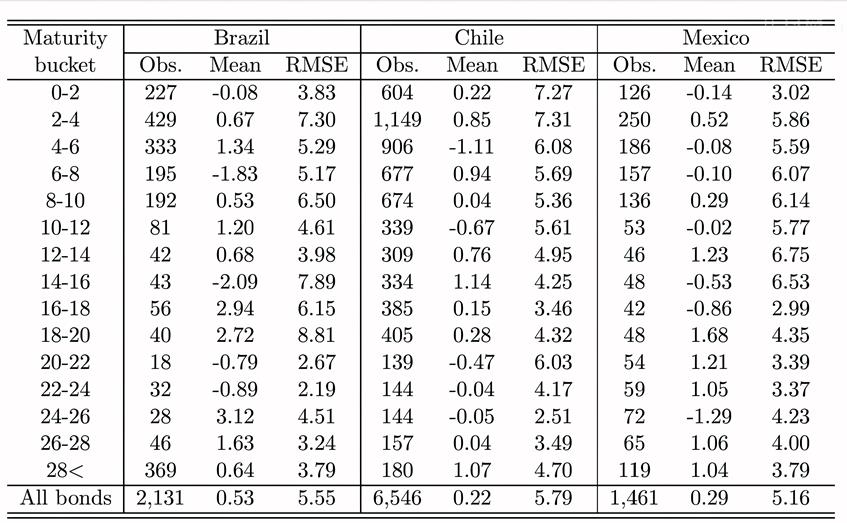
Nota. Esta tabla muestra el número de observaciones, la media de los errores de valoración (Media) y la raíz cuadrática media de los errores de valoración (RMSE) del modelo AFNS-L preferido para cada país. Los errores de valoración se expresan en puntos básicos y se calculan como la diferencia entre el rendimiento implícito observado de cada bono con cupón y su rendimiento implícito según el modelo.
En general, el ajuste del modelo es bastante bueno, con errores medios cuadrados muy bajos para todos los bonos combinados en los tres modelos. Esto sugiere que no hay componentes de riesgo en los residuos no explicados por el modelo. Además, el ajuste está equilibrado entre los vencimientos en los tres modelos. Por lo tanto, no hay ninguna parte de la curva de rendimiento que los modelos no sean capaces de ajustar.
En cuanto a las muestras individuales, observamos que los datos brasileños son relativamente escasos entre los plazos de 10 y 30 años. Como ya se ha mencionado al hablar de los valores λ, esto no impide que el modelo dé mucha importancia al ajuste de los precios de los bonos en ese segmento de la curva de rendimientos a través de su bajo valor para λ, como también indican los errores de ajuste relativamente modestos para los tramos de vencimiento asociados.
Los datos chilenos cubren bien toda la gama de vencimientos hasta 30 años. Además, como sugiere el bajo valor de λ en nuestro modelo chileno, éste pone más peso en el ajuste de los precios de los bonos a largo plazo. Esto explica sus pequeños errores de ajuste para los vencimientos a partir de 10 años.
4. PREMIO POR LIQUIDEZ DE LOS BONOS INDEXADOS A LA INFLACIÓN
En esta sección se examina los premios por liquidez indexados a la inflación que son específicas de cada bono y que se estiman mediante los modelos AFNS-L preferidos analizados en la sección anterior. Antes de estudiar la evolución histórica de los premios por riesgo de liquidez específicas de los bonos, primero los definimos explícitamente.
4.1. PREMIO POR LIQUIDEZ ESTIMADO DE LOS BONOS INDEXADOS A LA INFLACIÓN
Utilizando
los modelos AFNS-L estimados extraemos los premios por liquidez en cada mercado
de bonos indexados a la inflación. Para determinar el premio, primero
calculamos los precios ajustados de los bonos indexados a la inflación ![]() para
todos los valores existentes en nuestra muestra para el mercado dado utilizando
los parámetros estimados y los estados filtrados
para
todos los valores existentes en nuestra muestra para el mercado dado utilizando
los parámetros estimados y los estados filtrados ![]() . A
continuación, se resuelve un problema de punto fijo para convertir estos
precios de los bonos en rendimientos al vencimiento, o
. A
continuación, se resuelve un problema de punto fijo para convertir estos
precios de los bonos en rendimientos al vencimiento, o ![]() , mediante
la ecuación
, mediante
la ecuación
![]()
![]() ,
,
donde
![]() lo que indica que, si se
mantiene hasta el vencimiento,
lo que indica que, si se
mantiene hasta el vencimiento, ![]() es la tasa de rendimiento
real del i-ésimo bono (véase Sack & Elsasser 2004). Con el fin de obtener
los rendimientos asociados sin compensación por el riesgo de liquidez se genera
un nuevo conjunto de precios de bonos implícitos en el modelo a partir del
modelo AFNS-L estimado, pero sólo utilizando su componente sin fricciones, es
decir, utilizando las restricciones de que
es la tasa de rendimiento
real del i-ésimo bono (véase Sack & Elsasser 2004). Con el fin de obtener
los rendimientos asociados sin compensación por el riesgo de liquidez se genera
un nuevo conjunto de precios de bonos implícitos en el modelo a partir del
modelo AFNS-L estimado, pero sólo utilizando su componente sin fricciones, es
decir, utilizando las restricciones de que ![]() para
todo t, así como
para
todo t, así como ![]() y
y
![]() .
.
La
ecuación (5) se utiliza para convertir estos precios, que se representan como ![]() , en rendimientos al
vencimiento,
, en rendimientos al
vencimiento, ![]() Se trata de
aproximaciones a los precios que se cobrarían en ausencia de fricciones
financieras. A continuación, definimos el premio por liquidez del i-ésimo bono
como
Se trata de
aproximaciones a los precios que se cobrarían en ausencia de fricciones
financieras. A continuación, definimos el premio por liquidez del i-ésimo bono
como
![]()
El
premio por liquidez de los bonos indexados a la inflación, ![]() , para cada una de las
tres economías de nuestra muestra se presenta en cada momento del tiempo para
los bonos en circulación en la figura 2. Las tres series son positivas y han
mostrado cambios significativos a lo largo del tiempo, como cabría esperar de un
premio por riesgo. Además, observamos que su tamaño es significativo, con una
media de 144 puntos base, 115 puntos base y 60 puntos base para Brasil, Chile y
México, respectivamente. Así pues, premios por liquidez representan un
componente importante en todos estos rendimientos reales, tal como anticipan
los argumentos estructurales expuestos en Cardozo y Christensen (2023). A modo
de comparación, ese estudio reporta premios estimados para los bonos
colombianos indexados a la inflación, llamados bonos UVR, que promedian 225
puntos base con una desviación estándar de 32 puntos base durante el período
2005-2020. En general, consideramos que estos resultados implican que nuestros
premios estimados para los bonos indexados a la inflación son de un tamaño razonable
y se sitúan dentro del rango de estimaciones para otros mercados comparables de
bonos indexados a la inflación.
, para cada una de las
tres economías de nuestra muestra se presenta en cada momento del tiempo para
los bonos en circulación en la figura 2. Las tres series son positivas y han
mostrado cambios significativos a lo largo del tiempo, como cabría esperar de un
premio por riesgo. Además, observamos que su tamaño es significativo, con una
media de 144 puntos base, 115 puntos base y 60 puntos base para Brasil, Chile y
México, respectivamente. Así pues, premios por liquidez representan un
componente importante en todos estos rendimientos reales, tal como anticipan
los argumentos estructurales expuestos en Cardozo y Christensen (2023). A modo
de comparación, ese estudio reporta premios estimados para los bonos
colombianos indexados a la inflación, llamados bonos UVR, que promedian 225
puntos base con una desviación estándar de 32 puntos base durante el período
2005-2020. En general, consideramos que estos resultados implican que nuestros
premios estimados para los bonos indexados a la inflación son de un tamaño razonable
y se sitúan dentro del rango de estimaciones para otros mercados comparables de
bonos indexados a la inflación.
Figura 2
Premios por liquidez medias estimadas de los bonos indexados a la inflación
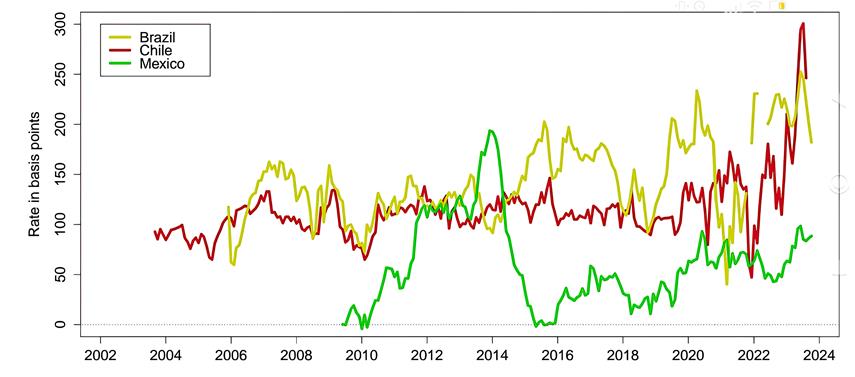
Nota. Gráfico que representa el premio por liquidez media estimada de los bonos indexados a la inflación para cada periodo en Brasil, Chile y México, tal como sugiere el modelo AFNS-L aumentado. Los premios de liquidez de los bonos indexados a la inflación se determinan estimando la diferencia de rendimiento entre el rendimiento al vencimiento ajustado de cada bono indexado a la inflación y el correspondiente rendimiento al vencimiento sin fricción con la característica de riesgo de liquidez desactivada.
5. ESTIMACIONES DE LA TASA REAL NATURAL BASADAS EN EL MERCADO
En esta sección definimos en primer lugar nuestra medida de la tasa real natural basada en medidas de mercado. A continuación, utilizamos nuestro modelo AFNS-L preferido para cada país con el fin de tener en cuenta la liquidez y los premios por plazo en los precios de los bonos indexados a la inflación. A partir de ahí, obtenemos las tasas reales esperadas de corto plazo y la correspondiente medida de la tasa real de equilibrio para cada uno de los tres países de nuestra muestra.
5.1. DEFINICIÓN DE LA TASA REAL NATURAL
Nuestra
definición de trabajo de la tasa de interés real de equilibrio ![]() es
es
![]()
es
decir, la tasa real media esperada a corto plazo durante un periodo de cinco
años vista que comienza con cinco años de antelación, cuando la previsión se
basa en la medida objetiva de probabilidad ℙ. Los shocks transitorios a
corto plazo deberían tener un impacto mínimo en esta tasa real de corto plazo
como se indica en CR. Una definición alternativa de ![]() sería la tasa real de
corto plazo estimada en un horizonte Infinito. Sin embargo, esta cifra
dependerá crucialmente de si la dinámica factorial presenta una raíz unitaria.
Es bien sabido que las duraciones medias de los datos de series temporales
disponibles no permiten distinguir de forma significativa entre procesos
estacionarios extremadamente persistentes y procesos no estacionarios. Dado que
nuestro modelo utiliza la primera estructura, nuestra tasa real predicha en
estado estacionario de horizonte infinito es, técnicamente hablando, constante,
en línea con la literatura financiera. Sin embargo, creemos que nuestras
muestras de datos carecen de información suficiente en el intervalo de
horizonte de 10 años al infinito para identificar adecuadamente ese estado
estacionario, por ello optamos por utilizar nuestra definición con un horizonte
de medio a largo plazo.
sería la tasa real de
corto plazo estimada en un horizonte Infinito. Sin embargo, esta cifra
dependerá crucialmente de si la dinámica factorial presenta una raíz unitaria.
Es bien sabido que las duraciones medias de los datos de series temporales
disponibles no permiten distinguir de forma significativa entre procesos
estacionarios extremadamente persistentes y procesos no estacionarios. Dado que
nuestro modelo utiliza la primera estructura, nuestra tasa real predicha en
estado estacionario de horizonte infinito es, técnicamente hablando, constante,
en línea con la literatura financiera. Sin embargo, creemos que nuestras
muestras de datos carecen de información suficiente en el intervalo de
horizonte de 10 años al infinito para identificar adecuadamente ese estado
estacionario, por ello optamos por utilizar nuestra definición con un horizonte
de medio a largo plazo.
5.2. ESTIMACIONES DE LA TASA REAL NATURAL
Utilizamos la tasa real media a corto plazo prevista para un período de cinco años, empezando a ser vista cinco años antes, como nuestra medida de la tasa real natural basada en el mercado. Esta está bien posicionada para representar las tendencias a largo plazo de la tasa real natural y no debería verse afectada por perturbaciones transitorias a corto plazo.
Para
ilustrar la descomposición subyacente a nuestra definición de ![]() recordemos que el premio
por plazo real se define como
recordemos que el premio
por plazo real se define como
![]()
Dicho
de otro modo, este premio es la diferencia en la rentabilidad real esperada
entre una estrategia de refinanciamiento periodo a periodo usando la tasa real
sin riesgo ![]() y
una estrategia de comprar y mantener un bono real a τ años. Subrayamos que
es el rendimiento real sin fricción el que se utiliza para calcular los premios
por plazo. En la figura 3 se muestra el desglose del modelo AFNS-L del
rendimiento real a 5 años en sus componentes para cada uno de los tres países.
En cada caso, el rendimiento sin ningún ajuste se muestra con una línea negra
continua. [14]
y
una estrategia de comprar y mantener un bono real a τ años. Subrayamos que
es el rendimiento real sin fricción el que se utiliza para calcular los premios
por plazo. En la figura 3 se muestra el desglose del modelo AFNS-L del
rendimiento real a 5 años en sus componentes para cada uno de los tres países.
En cada caso, el rendimiento sin ningún ajuste se muestra con una línea negra
continua. [14]
El
rendimiento real ajustado al modelo AFNS-L, o el rendimiento real sin
fricciones a 5 años, se muestra como una línea gris continua. Un indicador de
las fricciones del premio por liquidez en el punto de vencimiento a 5 años es
la diferencia entre el rendimiento real a plazo a 5 años y el rendimiento real
sin fricciones a 5 años, que se indica con sombreado amarillo. Obsérvese que
esta medida sintética a vencimiento constante de premios por liquidez diferente
de las medidas específicas de los bonos mostradas en la figura 2, ya que esta
última se ve afectada por la heterogeneidad en los tamaños de los cupones y el
tiempo restante hasta el vencimiento entre los bonos de nuestras muestras. Por
último, gracias a su coherencia teórica, el modelo AFNS-L proporciona una descomposición
del rendimiento real sin fricciones a 5 años en su componente de expectativas
de las tasas cortos reales y el premio temporal real residual basada en la
ecuación (8). En cada gráfico, la línea verde continua es el premio real a
plazo a 5 años, mientras que la línea azul continua es el componente de
expectativas, que es idéntico a nuestra definición de ![]()
En primer lugar, y lo que es más importante, observamos los considerables premios de liquidez de los bonos indexados a la inflación que abren una brecha entre el rendimiento real observado a 5 años y 5 años mostrado con una línea negra sólida y el rendimiento real inferior sin fricción a 5 años y 5 años mostrado con una línea gris sólida en los tres países. Por lo tanto, sin el ajuste de premios de liquidez, uno podría creer que los rendimientos reales son mucho más altos de lo que realmente son, un punto también señalado por Andreasen y Christensen (2016) en el contexto de los TIPS estadounidenses.
Para
Brasil, la descomposición del modelo produce una estimación de ![]() que fluctúa
significativamente con el ciclo económico en torno a una tendencia general más
baja. Comienza cerca del 7 por ciento a principios de 2006, pero luego cae
persistentemente hasta alcanzar un nivel inferior al 4 por ciento en los meses
previos a la pandemia en la primavera de 2020.[15]
Tras la reapertura económica después de la pandemia, nuestra estimación de
que fluctúa
significativamente con el ciclo económico en torno a una tendencia general más
baja. Comienza cerca del 7 por ciento a principios de 2006, pero luego cae
persistentemente hasta alcanzar un nivel inferior al 4 por ciento en los meses
previos a la pandemia en la primavera de 2020.[15]
Tras la reapertura económica después de la pandemia, nuestra estimación de ![]() sugiere que la tasa real
natural en Brasil ha vuelto a subir hasta alcanzar un nivel cercano al 4% y
medio al final de nuestra muestra. Por el contrario, el premio por plazo real
brasileño a 5 años se mantiene relativamente estable, salvo algunas
oscilaciones bruscas en los primeros años de nuestra muestra. Por último, la
tendencia al alza del premio por liquidez medio estimado específicamente de los
bonos en el gráfico 2 también es evidente en el premio por liquidez real
implícito brasileño a 5 años.
sugiere que la tasa real
natural en Brasil ha vuelto a subir hasta alcanzar un nivel cercano al 4% y
medio al final de nuestra muestra. Por el contrario, el premio por plazo real
brasileño a 5 años se mantiene relativamente estable, salvo algunas
oscilaciones bruscas en los primeros años de nuestra muestra. Por último, la
tendencia al alza del premio por liquidez medio estimado específicamente de los
bonos en el gráfico 2 también es evidente en el premio por liquidez real
implícito brasileño a 5 años.
Observamos
que, en el caso de Chile, a pesar del que el premio es volátil, oscila constantemente
en un nivel bastante estable desde principios de la década de 2000. Nuestra
estimación chilena sólo se ajusta parcialmente a las predicciones teóricas de
que el premio es contracíclico y aumenta durante las recesiones económicas. En comparación,
la línea azul, que representa la estimación chilena de la tasa natural de
interés predicha por el modelo AFNS-L, disminuye gradualmente desde
aproximadamente 0,5 por ciento a principios de la década de 2000 hasta menos de
-2 por ciento a mediados de 2022. Es importante destacar que se ha mantenido
bajo desde entonces a pesar de los grandes aumentos recientes de los
rendimientos de los bonos. Al final de nuestra muestra, la estimación chilena
de ![]() se sitúa en -1,30%.
se sitúa en -1,30%.
En
el caso de México, nuestra estimación de ![]() muestra un patrón
bastante constante y acíclico para la tasa real natural. En consecuencia, las
considerables fluctuaciones en los rendimientos reales sin fricción a 5 años en
México los cuales son después de contabilizar los cambios en los premios por liquidez
se deben a cambios en el premio por plazo real a 5 años en México, que con
frecuencia cambia de signo a diferencia de su contraparte chilena, que
permanece positiva a lo largo de nuestra muestra.
muestra un patrón
bastante constante y acíclico para la tasa real natural. En consecuencia, las
considerables fluctuaciones en los rendimientos reales sin fricción a 5 años en
México los cuales son después de contabilizar los cambios en los premios por liquidez
se deben a cambios en el premio por plazo real a 5 años en México, que con
frecuencia cambia de signo a diferencia de su contraparte chilena, que
permanece positiva a lo largo de nuestra muestra.
A continuación, ofrecemos una comparación directa de nuestras tres estimaciones de la tasa real natural, que se muestran en la figura 4. El grafico revela una diferencia marcada y fundamental entre estas tres economías latinoamericanas.
Figura 3
Descomposición de los rendimientos reales 5yr5yr
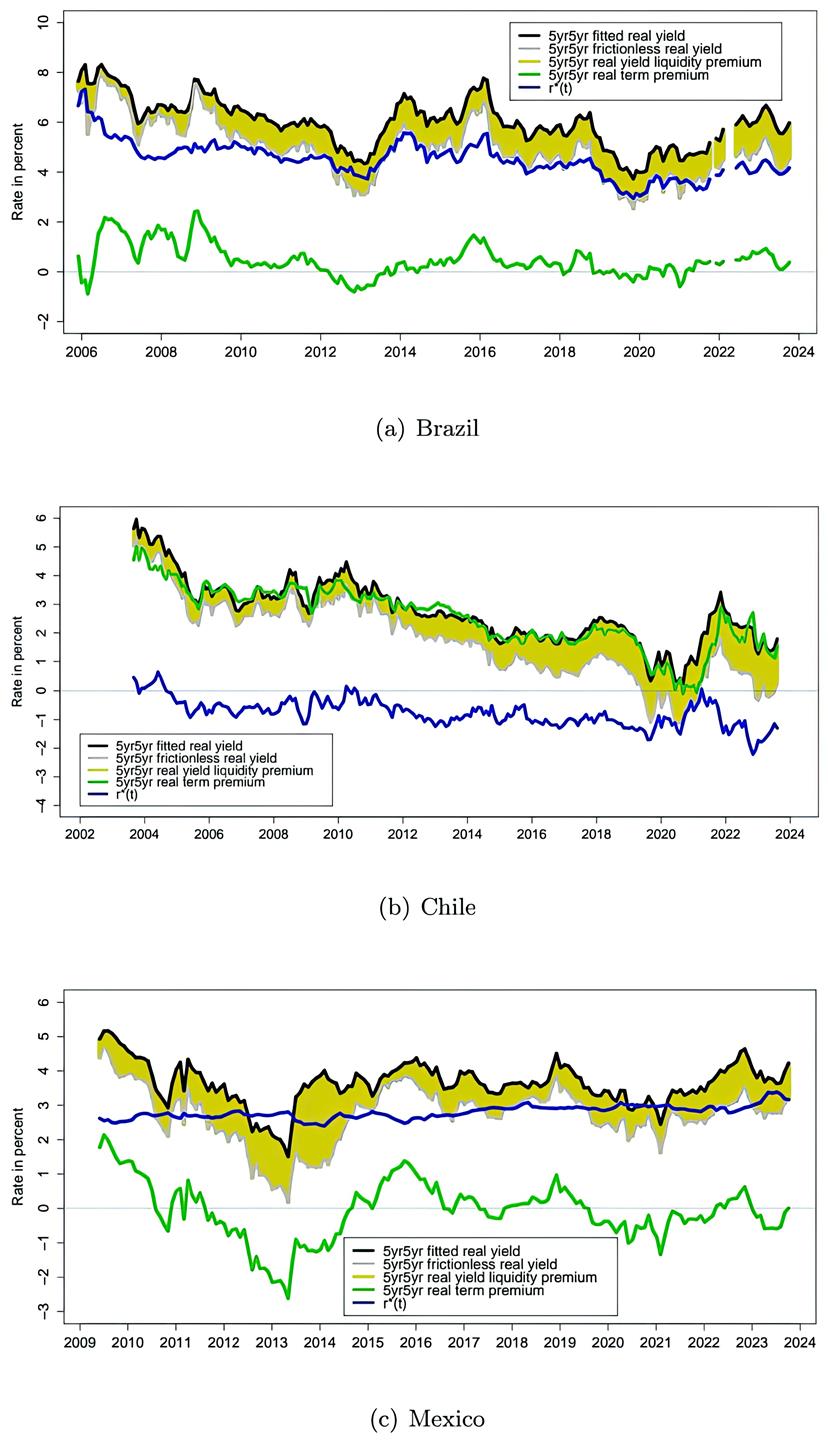
Figura 4
Comparación
de las estimaciones de ![]() basadas en el mercado
basadas en el mercado
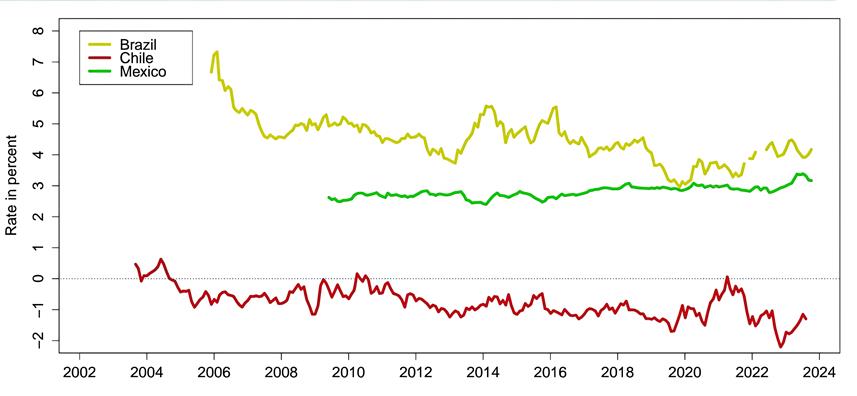
La
magnitud y la variación de ![]() en
Brasil apuntan a una cierta inestabilidad de las condiciones económicas
fundamentales en ese país. Esto contrasta fuertemente con los resultados para
México, que sugieren que las condiciones económicas son más estables allí. Sin
embargo, el elevado nivel de
en
Brasil apuntan a una cierta inestabilidad de las condiciones económicas
fundamentales en ese país. Esto contrasta fuertemente con los resultados para
México, que sugieren que las condiciones económicas son más estables allí. Sin
embargo, el elevado nivel de ![]() en
México, con un valor cercano al 3%, sigue apuntando a cierta fragilidad
económica en relación con las economías avanzadas, donde
en
México, con un valor cercano al 3%, sigue apuntando a cierta fragilidad
económica en relación con las economías avanzadas, donde ![]() suele
ser más bajo, véase Holston et al. (2017). En este contexto, y dado que Chile
es la principal economía de América Latina, no es sorprendente ver que la tasa
real natural chilena es mucho más baja y, con pocas excepciones, se ha
mantenido negativa durante casi 20 años. Además, observamos que Ceballos et al.
(2024) encuentran que su estimación chilena de
suele
ser más bajo, véase Holston et al. (2017). En este contexto, y dado que Chile
es la principal economía de América Latina, no es sorprendente ver que la tasa
real natural chilena es mucho más baja y, con pocas excepciones, se ha
mantenido negativa durante casi 20 años. Además, observamos que Ceballos et al.
(2024) encuentran que su estimación chilena de ![]() ,
que
es similar a la nuestra, sigue tendencias ampliamente similares a una
estimación de base macro de
,
que
es similar a la nuestra, sigue tendencias ampliamente similares a una
estimación de base macro de ![]() para
Chile utilizando el enfoque de Holston et al. (2017). También encuentran que su
estimación de
para
Chile utilizando el enfoque de Holston et al. (2017). También encuentran que su
estimación de ![]() es
similar a una estimación colombiana basada en el mercado calculada a partir de
una actualización del análisis de Cardozo y Christensen (2023). Además. la
estimación
es
similar a una estimación colombiana basada en el mercado calculada a partir de
una actualización del análisis de Cardozo y Christensen (2023). Además. la
estimación ![]() de nuestro modelo AFNS-L
preferido para México es muy cercana a la estimación basada en el mercado
reportada por Beauregard et al. (2023), aunque ellos utilizan una combinación
de precios de bonos nominales mexicanos y precios de bonos mexicanos indexados
a la inflación para su análisis. Por lo tanto, consideramos que nuestras
estimaciones de
de nuestro modelo AFNS-L
preferido para México es muy cercana a la estimación basada en el mercado
reportada por Beauregard et al. (2023), aunque ellos utilizan una combinación
de precios de bonos nominales mexicanos y precios de bonos mexicanos indexados
a la inflación para su análisis. Por lo tanto, consideramos que nuestras
estimaciones de ![]() tienen un tamaño
razonable y son representativas de las estimaciones publicadas en la literatura
para nuestra muestra de países.
tienen un tamaño
razonable y son representativas de las estimaciones publicadas en la literatura
para nuestra muestra de países.
Por
último, es interesante observar que los aumentos de las tasas de interés y el
consiguiente deterioro de las condiciones financieras en respuesta al período
de elevada inflación tras la reapertura económica después de la pandemia de
COVID-19 parecen haber levemente nuestras estimaciones de ![]() Esto sugiere que las tasas
de interés en estos tres países volverán a situarse en niveles más bajos una
vez que la inflación haya vuelto al objetivo fijado por sus respectivos bancos
centrales. Además, añadimos que la dinámica factorial estimada de nuestros
modelos AFNS-L preferidos podría aprovecharse para hacer proyecciones de
Esto sugiere que las tasas
de interés en estos tres países volverán a situarse en niveles más bajos una
vez que la inflación haya vuelto al objetivo fijado por sus respectivos bancos
centrales. Además, añadimos que la dinámica factorial estimada de nuestros
modelos AFNS-L preferidos podría aprovecharse para hacer proyecciones de ![]() en el futuro, como se
hace en Ceballos et al. (2024). Sin embargo, aunque tales proyecciones podrían
ser de enorme importancia tanto para la política fiscal y monetaria como para
la gestión de activos a largo plazo, dejamos esa tarea para futuros trabajos
con el fin de ahorrar espacio.
en el futuro, como se
hace en Ceballos et al. (2024). Sin embargo, aunque tales proyecciones podrían
ser de enorme importancia tanto para la política fiscal y monetaria como para
la gestión de activos a largo plazo, dejamos esa tarea para futuros trabajos
con el fin de ahorrar espacio.
Desde
un punto de vista práctico, insistimos en que estas estimaciones conllevan una
incertidumbre considerable. Por desgracia, no existe un método estándar para
calcular sus intervalos de confianza. Sin embargo, CR utiliza simulaciones para
examinar el rol de la incertidumbre de los parámetros en sus estimaciones de ![]() y constata que su
impacto es bastante considerable. A esto hay que añadir los efectos no
cuantificados de la incertidumbre del modelo y de la medición. Así pues, la
recomendación general sería evitar hacer hincapié en cualquier estimación
puntual individual y, en su lugar, centrarse en las tendencias más amplias de
las series temporales, de forma similar a nuestra descripción anterior.
y constata que su
impacto es bastante considerable. A esto hay que añadir los efectos no
cuantificados de la incertidumbre del modelo y de la medición. Así pues, la
recomendación general sería evitar hacer hincapié en cualquier estimación
puntual individual y, en su lugar, centrarse en las tendencias más amplias de
las series temporales, de forma similar a nuestra descripción anterior.
5.3. ORIENTACIÓN DE LA POLÍTICA MONETARIA
Como
ejercicio final, utilizamos nuestras estimaciones de ![]() para obtener una medida
de la orientación de la política monetaria en las tres economías analizadas.
Esto también ofrece una forma alternativa de validar nuestro enfoque para
estimar
para obtener una medida
de la orientación de la política monetaria en las tres economías analizadas.
Esto también ofrece una forma alternativa de validar nuestro enfoque para
estimar ![]()
Como
se señaló en la introducción, las estimaciones de la tasa real natural
desempeñan un papel clave en las reglas de política monetaria como indicador
por encima del cual la tasa real a corto plazo ![]() se
consideraría restrictiva, mientras que las que se sitúan por debajo se
asociarían a una orientación acomodaticia de la política monetaria. Así, la
orientación de la política monetaria puede medirse como
se
consideraría restrictiva, mientras que las que se sitúan por debajo se
asociarían a una orientación acomodaticia de la política monetaria. Así, la
orientación de la política monetaria puede medirse como
![]()
Sin
embargo, es importante señalar que, gracias al comportamiento prospectivo de
las empresas, sus trabajadores y los inversionistas en general, no es la tasa
de interés real a corto plazo la que importa para una serie de decisiones
económicas, sino la que probablemente prevalezca en los próximos trimestres.
Por lo tanto, para cuantificar la orientación de la política monetaria,
consideramos dos aproximaciones para ![]() . Una es una medida
tomada de Werner (2023) que explota la ecuación de Fischer descontando la tasa
de política nominal anualizado con la inflación esperada a 12 meses, mientras
que la otra es el rendimiento real a 12 meses a partir de nuestros datos de
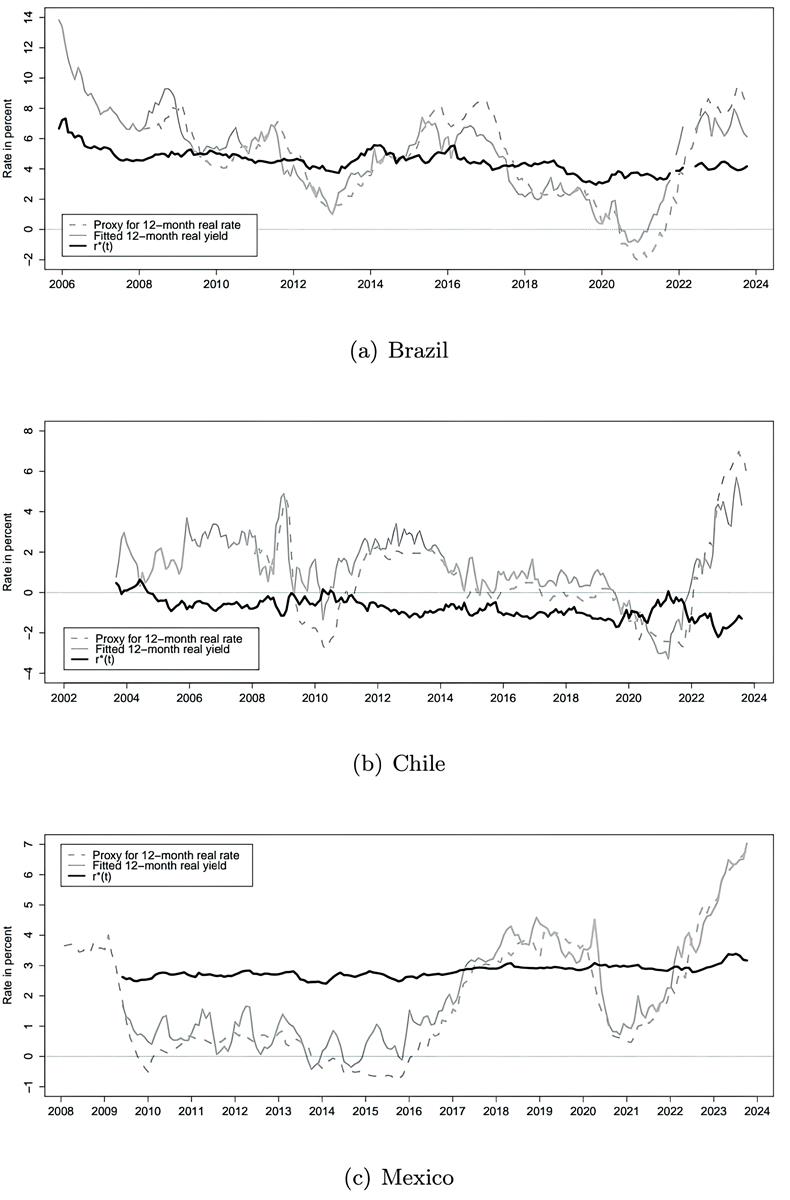
bonos sin ningún ajuste, como en Christensen y Mouabbi (2024).[16]
Estas medidas de
. Una es una medida
tomada de Werner (2023) que explota la ecuación de Fischer descontando la tasa
de política nominal anualizado con la inflación esperada a 12 meses, mientras
que la otra es el rendimiento real a 12 meses a partir de nuestros datos de
bonos sin ningún ajuste, como en Christensen y Mouabbi (2024).[16]
Estas medidas de ![]() y la estimación asociada
de
y la estimación asociada
de ![]() se muestran en la figura
5 para cada uno de los tres países de nuestra muestra.
se muestran en la figura
5 para cada uno de los tres países de nuestra muestra.
Algunos rasgos comunes son notables. En primer lugar, la política monetaria alcanzó una orientación acomodaticia relativamente pronto durante el periodo pandémico en los tres países. Además, al final de nuestra muestra, la política monetaria parece ser muy restrictiva en términos históricos. Esto subraya el argumento de Werner (2023) de que, a medida que la inflación disminuye gradualmente hacia el objetivo oficial de inflación en las tres economías, las tasas de interés a un día deben reducirse paralelamente para evitar que la política monetaria se vuelva excesivamente restrictiva.
Por
último, a pesar de las grandes oscilaciones de los rendimientos reales a corto
plazo en las tres economías desde 2020, nuestras estimaciones de la tasa real
natural ![]() han variado muy poco, y
al final de nuestras muestras están todas cerca de donde estaban a principios
de 2020. Esto sugiere que ni en el periodo de la pandemia ni en el inesperado
repunte de la inflación tras la reapertura económica y el consiguiente
endurecimiento de la política monetaria han dejado huellas significativas en la
tasa de interés real en estado estacionario de estos tres países. Dado que son países
representativos tanto de América Latina como de economías de mercado emergentes
en general, nuestras conclusiones pueden extenderse mucho más allá de la
muestra de países aquí examinada. Sin embargo, dejamos para futuras
investigaciones la exploración de esta conjetura.
han variado muy poco, y
al final de nuestras muestras están todas cerca de donde estaban a principios
de 2020. Esto sugiere que ni en el periodo de la pandemia ni en el inesperado
repunte de la inflación tras la reapertura económica y el consiguiente
endurecimiento de la política monetaria han dejado huellas significativas en la
tasa de interés real en estado estacionario de estos tres países. Dado que son países
representativos tanto de América Latina como de economías de mercado emergentes
en general, nuestras conclusiones pueden extenderse mucho más allá de la
muestra de países aquí examinada. Sin embargo, dejamos para futuras
investigaciones la exploración de esta conjetura.
Figura 5
Medidas
de los rendimientos reales a corto plazo y ![]()
6. CONCLUSIÓN
En la literatura existente, la mayoría de las estimaciones del nivel de la tasa real de corto plazo en estado estacionario están basadas en modelos macroeconómicos. Sin embargo, la incertidumbre sobre la especificación macroeconómica correcta, en particular durante la pandemia de COVID-19, plantea interrogantes sobre las estimaciones macroeconómicas resultantes de la tasa real natural. En este artículo evitamos este problema centrándonos en una medida financiera de la tasa real de equilibrio que se basa en modelos empíricos que se estructuran con términos dinámicos estimados únicamente con los precios de bonos indexados a la inflación. Al ajustar tanto los premios por liquidez de los bonos indexados a la inflación como los premios por plazo real, descubrimos las expectativas subyacentes de los inversionistas sobre los premios de tasa reales de corto plazo sin fricciones para un período de cinco años que comienza dentro de cinco años. Además, nuestro estudio es único en el sentido de que aplicamos este enfoque a tres importantes economías latinoamericanas: Brasil, Chile y México.
En primer lugar, documentamos premios por riesgo de liquidez amplios y variables en el tiempo en los tres mercados de bonos, con pocos puntos en común. Por lo tanto, nuestro estudio proporciona apoyo empírico a los argumentos expuestos en Cardozo y Christensen (2023), implicando que las tenencias de bonos indexados a la inflación deberían concentrarse entre inversionistas nacionales pacientes que compran y mantienen, como los fondos de pensiones. Como resultado, los bonos indexados a la inflación deberían negociarse menos que los bonos nominales estándar y enfrentarse a importantes riesgos de liquidez, consistente con nuestros resultados. Es importante destacar que esta lógica y nuestros resultados también implican que es probable que los tres mercados de bonos indexados estén realmente dominados por inversores nacionales. En consecuencia, la información sobre el precio de los bonos debería reflejar las expectativas de la tasa reales y el apetito por el riesgo de los inversores nacionales, un supuesto clave que subyace en nuestra elección de analizar cada país por separado.
En
un segundo paso, procedemos a ajustar los rendimientos reales sin fricción
ajustados a la liquidez para los premios por plazo reales incorporados, con el
fin de obtener nuestras estimaciones de la tasa de interés real natural para
cada país. De acuerdo con la intuición anterior, nuestras estimaciones de ![]() parecen
ser únicas para cada país y bastante dispersas. Nuestra estimación para Brasil
es alta en promedio, con grandes fluctuaciones cíclicas. En cambio, nuestra
estimación para México es muy estable, aunque elevada en comparación con los
estándares internacionales. Por último, nuestra estimación de
parecen
ser únicas para cada país y bastante dispersas. Nuestra estimación para Brasil
es alta en promedio, con grandes fluctuaciones cíclicas. En cambio, nuestra
estimación para México es muy estable, aunque elevada en comparación con los
estándares internacionales. Por último, nuestra estimación de ![]() para
Chile se asemeja a las comunicadas para las economías avanzadas, por ejemplo,
como en CR, al ser baja y caracterizarse por un descenso gradual persistente
durante los últimos 20 años. La gran dispersión en las estimaciones de la tasa
real natural en estas tres economías parece coherente con las notables
diferencias en sus fundamentos económicos y su nivel general de desarrollo
económico. Sin embargo, dejamos para futuras investigaciones la interrogante de
cómo se correlacionan exactamente las diferencias documentadas en las
estimaciones de
para
Chile se asemeja a las comunicadas para las economías avanzadas, por ejemplo,
como en CR, al ser baja y caracterizarse por un descenso gradual persistente
durante los últimos 20 años. La gran dispersión en las estimaciones de la tasa
real natural en estas tres economías parece coherente con las notables
diferencias en sus fundamentos económicos y su nivel general de desarrollo
económico. Sin embargo, dejamos para futuras investigaciones la interrogante de
cómo se correlacionan exactamente las diferencias documentadas en las
estimaciones de ![]() con
los fundamentos económicos.
con
los fundamentos económicos.
También
es probable que la dispersión documentada en ![]() tenga
implicaciones bastante diferentes para la ejecución de la política monetaria en
estos tres países. Sin embargo, a tal fin, debe tenerse presente la notable
incertidumbre que rodea a estas estimaciones, como también se subraya en
Holston et al. (2017).
tenga
implicaciones bastante diferentes para la ejecución de la política monetaria en
estos tres países. Sin embargo, a tal fin, debe tenerse presente la notable
incertidumbre que rodea a estas estimaciones, como también se subraya en
Holston et al. (2017).
Además,
destacamos que nuestro enfoque basado en el mercado para estimar ![]() puede
aplicarse tanto a las economías avanzadas como a las emergentes. Sin embargo,
volvemos a dejar para futuras investigaciones la verificación de si nuestras
conclusiones se extienden más allá de las tres principales economías
latinoamericanas aquí examinadas.
puede
aplicarse tanto a las economías avanzadas como a las emergentes. Sin embargo,
volvemos a dejar para futuras investigaciones la verificación de si nuestras
conclusiones se extienden más allá de las tres principales economías
latinoamericanas aquí examinadas.
Por último, nuestras estimaciones de la tasa de interés natural podrían ser una herramienta valiosa para el análisis de la política monetaria en tiempo real, ya que se basan en la información prospectiva que se valora en los mercados activos de bonos indexados a la inflación de estos tres países y que puede actualizarse diariamente. Dejamos la exploración de tales aplicaciones para futuras investigaciones.
APÉNDICE A: BONOS INDEXADOS A LA INFLACIÓN EN BRASIL
Figura A1
Bonos indexados a la inflación en Brasil
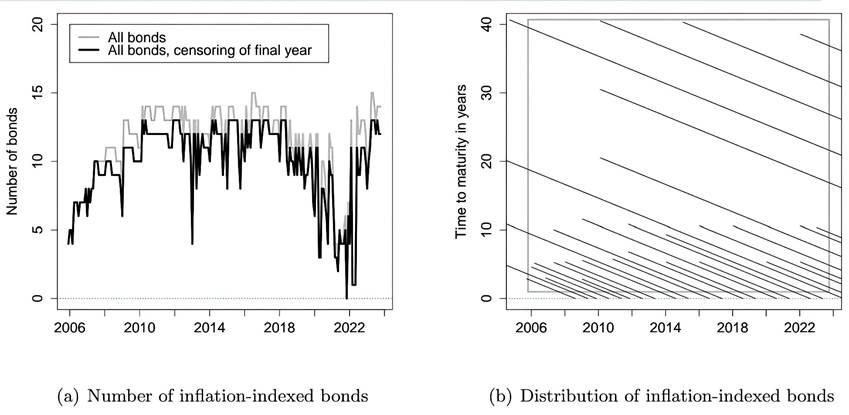
Nota. La cantidad de bonos brasileños indexados a la inflación que están en circulación en un momento dado se muestra en el panel (a). El panel (b) muestra la distribución de vencimientos de todos los bonos brasileños indexados a la inflación emitidos desde 2006. La muestra del análisis, que se limita a los precios de los bonos indexados a la inflación con más de un año de vencimiento, está representada por el rectángulo gris sólido. La muestra se inició el 30 de noviembre de 2005 y finaliza el 30 de septiembre de 2023.
Debido a su experiencia con largos periodos de inflación extremadamente elevada, Brasil tiene una larga historia de emisión de bonos indexados a la inflación como instrumento clave para financiar la deuda pública. Estos bonos se conocen como Notas do Tesouro Nacional Serie B, o NTNB, y sus pagos de cupón y principal están indexados al IPCA, que es el principal índice de precios al consumidor brasileño y el objetivo del Banco Central de Brasil a la hora de fijar la política monetaria. Como señalan Kubudi y Vicente (2016), el mercado de estos bonos es el quinto mayor mercado de bonos indexados a la inflación del mundo.
La línea gris continua de la figura A1(a) representa el número total de bonos brasileños indexados a la inflación en circulación a lo largo del tiempo en nuestra muestra. En septiembre de 2023, cuando finaliza nuestro periodo de estudio, había 14 bonos en circulación. Dicho esto, debido al desfase de indexación en sus pagos, los precios de los bonos indexados a la inflación que se acercan a su vencimiento tienden a ser un poco inestables, como mencionaron Gürkaynak et al. (2010) y ACR. Por lo tanto, eliminamos los bonos indexados a la inflación de nuestra muestra en el momento en que les queda menos de un año para su fecha de vencimiento con el fin de facilitar la estimación del modelo.
La línea negra continua de la figura A1(a) ilustra cómo el número de bonos de la muestra se reduce algo tras aplicar este umbral. La información contractual de cada uno de los 31 BNA de nuestros datos, junto con la cantidad de observaciones mensuales de cada uno, se incluye finalmente en la tabla A1. Un aspecto distintivo de este mercado es que todos los bonos tienen la misma tasa de cupón anual del 6%, que se paga semestralmente.
Normalmente, el gobierno brasileño ha subastado una serie de bonos indexados a la inflación, con vencimientos iniciales que oscilan entre tres y 41 años. La figura A1(b) muestra la distribución de vencimientos de los 31 bonos de nuestra muestra. Una única línea descendente que muestra los años restantes hasta el vencimiento del bono para cada fecha sirve de representación. El universo de bonos disponible ofrece una buena cobertura de nuestra muestra, en particular para los vencimientos de cinco a diez años de gran interés para nuestra investigación.
Tabla A1
Muestra de bonos brasileños indexados a la inflación
|
Inflation-indexed bond |
Issuance Date |
No. obs. |
|
(1) 6% 5/15/2009 |
9/15/2003 |
29 |
|
(2) 6% 8/15/2024 |
10/15/2003 |
193 |
|
(3) 6% 5/15/2015 |
10/15/2003 |
101 |
|
(4) 6% 5/15/2045 |
9/15/2004 |
171 |
|
(5) 6% 8/15/2008 |
9/15/2005 |
19 |
|
(6) 6% 8/15/2010 |
1/5/2006 |
41 |
|
(7) 6% 5/15/2011 |
3/9/2006 |
50 |
|
(8) 6% 11/15/2009 |
11/9/2006 |
24 |
|
(9) 6% 5/15/2017 |
5/9/2007 |
107 |
|
(10) 6% 8/15/2012 |
5/9/2007 |
51 |
|
(11) 6% 5/15/2013 |
1/9/2008 |
52 |
|
(12) 6% 8/15/2020 |
1/14/2009 |
126 |
|
(13) 6% 11/15/2011 |
1/14/2009 |
22 |
|
(14) 6% 8/15/2014 |
1/14/2009 |
55 |
|
(15) 6% 8/15/2050 |
2/10/2010 |
117 |
|
(16) 6% 8/15/2030 |
2/10/2010 |
129 |
|
(17) 6% 8/15/2040 |
2/10/2010 |
116 |
|
(18) 6% 8/15/2016 |
11/10/2010 |
57 |
|
(19) 6% 8/15/2022 |
10/13/2011 |
114 |
|
(20) 6% 8/15/2018 |
10/13/2011 |
68 |
|
(21) 6% 5/15/2023 |
1/15/2014 |
88 |
|
(22) 6% 5/15/2019 |
1/15/2014 |
52 |
|
(23) 6% 5/15/2055 |
1/14/2015 |
85 |
|
(24) 6% 8/15/2026 |
1/6/2016 |
76 |
|
(25) 6% 5/15/2021 |
1/6/2016 |
52 |
|
(26) 6% 8/15/2028 |
1/10/2018 |
50 |
|
(27) 6% 5/15/2025 |
1/8/2020 |
29 |
|
(28) 6% 8/15/2032 |
1/5/2022 |
17 |
|
(29) 6% 8/15/2060 |
1/12/2022 |
21 |
|
(30) 6% 5/15/2027 |
1/12/2022 |
16 |
|
(31) 6% 5/15/2033 |
1/4/2023 |
6 |
Nota. Para cada bono a lo largo del periodo de muestra, desde el 30 de noviembre de 2005 hasta el 30 de septiembre de 2023, la tabla proporciona información sobre sus atributos, fecha de primera emisión y número de fechas de observación mensual.
APÉNDICE B: RESULTADOS DE LA SELECCIÓN DE MODELOS
Tabla B1
Evaluación de especificaciones alternativas del modelo brasileño AFNS-L
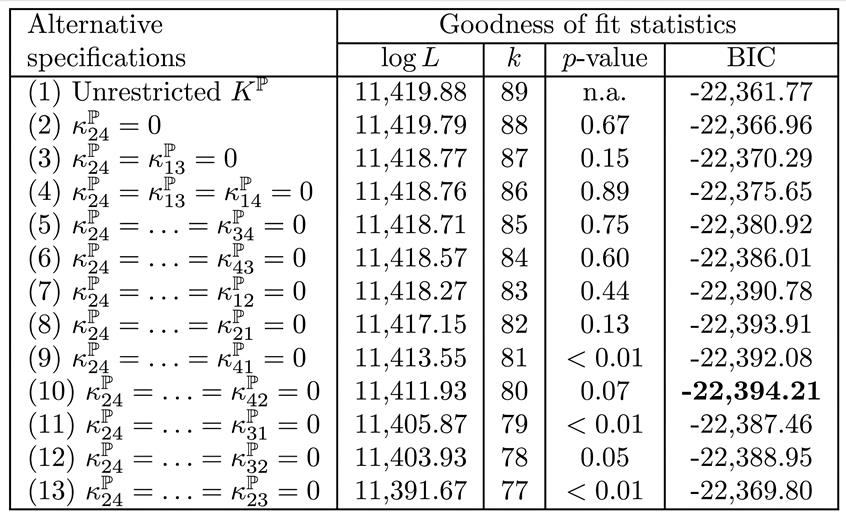
Nota. En el modelo brasileño AFNS-L hay trece especificaciones estimadas diferentes. En cada especificación se incluye la máxima verosimilitud logarítmica (log L), el número de parámetros (k), el criterio de información bayesiano (BIC) y el valor p de una prueba de razón de verosimilitud de la hipótesis de que difiere de la especificación anterior con un parámetro libre más. El análisis abarca desde el 30 de noviembre de 2005 hasta el 30 de septiembre de 2023, con datos mensuales.
Tabla B2
Evaluación de especificaciones alternativas del modelo AFNS-L chileno
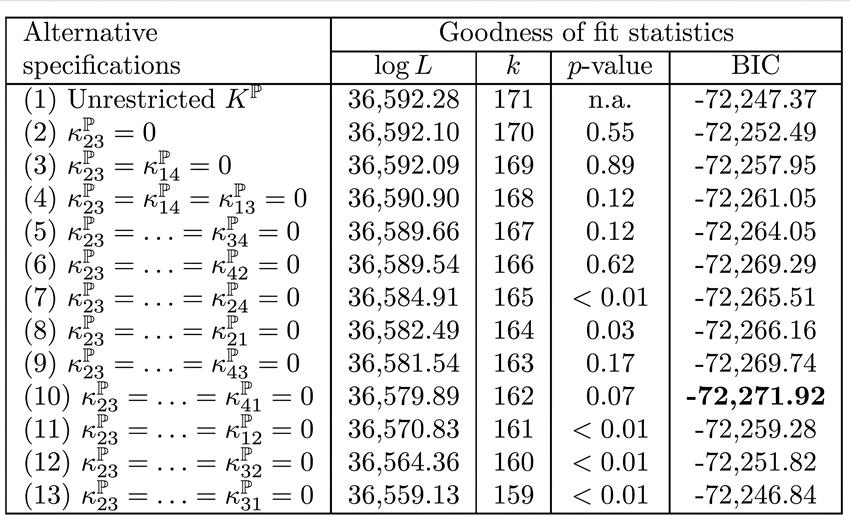
Nota. Hay trece especificaciones estimadas diferentes para el modelo chileno AFNS-L. Para cada especificación, se proporciona la siguiente información: la máxima verosimilitud logarítmica (log L), el número de parámetros (k), el valor p de una prueba de razón de verosimilitud sobre la hipótesis de que la especificación varía de la anterior en un parámetro libre, y el criterio de información bayesiano (BIC). En el periodo de análisis se incluyen datos mensuales desde el 31 de agosto de 2003 hasta el 31 de julio de 2023.
Tabla B3
Evaluación de especificaciones alternativas del modelo mexicano AFNS-L
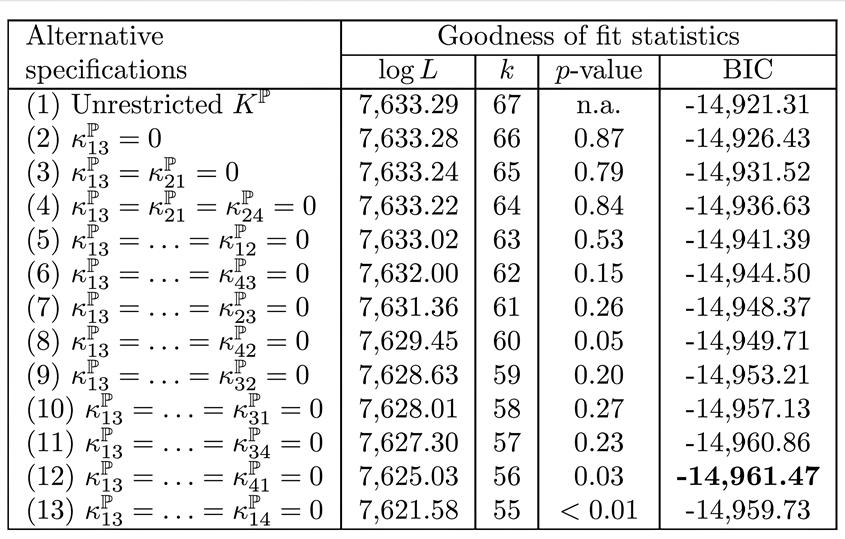
Nota. Hay trece especificaciones estimadas distintas para la variante mexicana AFNS-L. Para cada especificación, se proporciona la siguiente información: la máxima verosimilitud logarítmica (log L), el número de parámetros (k), el valor p de una prueba de razón de verosimilitud sobre la hipótesis de que la especificación varía de la anterior en un parámetro libre, y el criterio de información bayesiano (BIC). En el periodo de análisis se incluyen datos mensuales desde el 31 de mayo de 2009 hasta el 29 de septiembre de 2023.
REFERENCIAS
Andreasen, M. M., & Christensen, J. H. (2016). TIPS liquidity and the outlook for inflation. FRBSF Economic Letter, 35, 1-5. https://www.frbsf.org/economic-research/wp-content/uploads/sites/4/el2016-35.pdf
Andreasen, M. M., Christensen, J. H., & Riddell, S. (2021). The TIPS liquidity premium. Review of Finance, 25(6), 1639-1675. https://doi.org/10.1093/rof/rfab018
Andreasen, M. M., Christensen, J. H., & Rudebusch, G. D. (2019). Term structure analysis with big data : one-step estimation using bond prices. Journal of Econometrics, 212(1), 26-46. https://doi.org/10.1016/j.jeconom.2019.04.019
Arida, P., Bacha, E. L., & Lara-Resende, A. (2005). Credit, interest, and jurisdictional uncertainty : conjectures on the case of Brazil. In Inflation Targeting, Debt, and the Brazilian Experience, 1999 to 2003, edited by F. Giavazzi, I. Goldfajn, and S. Herrera. Cambridge, MA : MIT Press, 265-293 (Chapter 8).
Bacha, E. L., Holland, M., & Gonçalves, F. M. (2009). A panel-data analysis of interest rates and dollarization in Brazil. Revista Brasileira de Economia, Vol. 63, No. 4, 341–360.
Barbosa, F. de H. (2006). The contagion effect of public debt on monetary policy : the Brazilian experience. Brazilian Journal of Political Economy, Vol. 26, No. 2, 231-238.
Beauregard, R., Christensen, J. H. E., Fischer, E., & Zhu, S. (2021). Inflation expectations and risk premia in emerging bond markets : evidence from Mexico. FRB of New York Staff Report, (961). https://dx.doi.org/10.2139/ssrn.3808273
Blake, A. P., Rule, G. R., & Rummel, O. J. (2015). Inflation targeting and term premia estimates for Latin America. Latin American Economic Review, 24(1), 1-21. https://doi.org/10.1007/s40503-015-0017-7
Cardozo, C. H. R., & Christensen, J. H. E. (2023). The benefit of inflation-indexed debt : evidence from an emerging bond market. Federal Reserve Bank of San Francisco Working Paper 2023-04. https://doi.org/10.24148/wp2023-04
Ceballos, L., Christensen, J. H. E. & Romero D. (2024). A post-pandemic new normal for interest rates in emerging bond markets ? Evidence from Chile. Mimeo
Ceballos, L., Naudon, A. & Romero, D. (2016). Nominal term structure and term premia : evidence from Chile. Applied Economics, Vol. 48, No. 29, 2721-2735.
Christensen, J. H., Diebold, F. X., & Rudebusch, G. D. (2011). The affine arbitrage-free class of Nelson–Siegel term structure models. Journal of Econometrics, 164(1), 4-20. https://doi.org/10.1016/j.jeconom.2011.02.011
Christensen, J. H., Lopez, J. A., & Rudebusch, G. D. (2014). Do central bank liquidity facilities affect interbank lending rates ? Journal of Business & Economic Statistics, 32(1), 136-151. https://doi.org/10.1080/07350015.2013.858631
Christensen, J. H., & Rudebusch, G. D. (2019). A new normal for interest rates ? Evidence from inflation-indexed debt. Review of Economics and Statistics, 101(5), 933-949https://doi.org/10.1162/rest_a_00821
Clarida, R. (2014). Navigating the new neutral. Economic Outlook, PIMCO.
Dai, Q., & Singleton, K. J. (2000). Specification analysis of affine term structure models. The journal of finance, 55(5), 1943-1978. https://doi.org/10.1111/0022-1082.00278
De Pooter, M., Robitaille, P. T., Walker, I., & Zdinak, M. (2014). Are long-term inflation expectations well anchored in Brazil, Chile and Mexico ? International Journal of Central Banking, 10(2), 337-400. https://ssrn.com/abstract=2572011
Duffee, G. R. (2002). Term premia and interest rate forecasts in affine models. The Journal of Finance, 57(1), 405-443. https://doi.org/10.1111/1540-6261.00426
Eggertsson, G. B., Mehrotra, N. R., Singh, S. R., & Summers, L. H. (2016). A contagious malady ? Open economy dimensions of secular stagnation. IMF Economic Review, 64(4), 581-634. https://doi.org/10.1057/s41308-016-0019-8
Finlay, R., & Wende, S. (2012). Estimating inflation expectations with a limited number of inflation-indexed bonds. International Journal of Central Banking, 8(2), 111-142. https://www.ijcb.org/journal/ijcb12q2a4.htm
Gonçalves, F. M., Holland, M., & Spacov, A. D. (2007). Can jurisdictional uncertainty and capital controls explain the high level of real interest rates in Brazil ? Evidence from panel data. Revista Brasileira de Economia, Vol. 61, No. 1, 49-75.
Grishchenko, O. V., & Huang, J. Z. (2013). Inflation risk premium : evidence from the TIPS market. Journal of Fixed Income, 22(4), 5-30. http://dx.doi.org/10.3905/jfi.2013.22.4.005
Gürkaynak, R. S., Sack, B., & Wright, J. H. (2010). The TIPS yield curve and inflation compensation. American Economic Journal : Macroeconomics, 2(1), 70-92. http://dx.doi.org/10.1257/mac.2.1.70
Hamilton, J. D., Harris, E. S., Hatzius, J., & West, K. D. (2016). The equilibrium real funds rate : past, present, and future. IMF Economic Review, 64, 660-707. https://doi.org/10.1057/s41308-016-0015-z
Holston, K., Laubach, T., & Williams, J. C. (2017). Measuring the natural rate of interest : international trends and determinants. Journal of International Economics, 108(1), S59-S75. https://doi.org/10.1016/j.jinteco.2017.01.004
Kim, D. H., & Singleton, K. J. (2012). Term structure models and the zero bound : an empirical investigation of Japanese Yields. Journal of Econometrics, 170(1), 32-49. https://doi.org/10.1016/j.jeconom.2011.12.005
Kubudi, D., & Vicente, J. (2016). A joint model of nominal and real yield curves. Banco Central do Brasil Working Paper Series No. 452.
Nelson, C. R., & Siegel, A. F. (1987). Parsimonious modeling of yield curves. Journal of business, 60(4), 473-489. https://www.jstor.org/stable/2352957
Orphanides, A., & Williams, J. C. (2002). Robust monetary policy rules with unknown natural rates. Brookings Papers on Economic Activity, 2002(2), 63-145. https://doi.org/10.1353/eca.2003.0007
Perrelli, R., & Roache, S. K. (2014). Time-varying neutral interest rate---the case of Brazil. IMF Working Paper 14/84.
Sack, B. P., & Elsasser, R. (2004). Treasury inflation-indexed debt : review of the US experience. Economic Policy Review, 10(1). https://ssrn.com/abstract=788044
Werner, A. (2023). Monetary policy in Latin America : the easing cycle has begun. Policy Brief 23-16, Peterson Institute for International Economics.