Revista IECOS, 24(2), 79-100
CONVERGENCIA DE PROCESOS ALEATORIOS UNIDIMENSIONALES
CONVERGENCE OF ONE-DIMENSIONAL RANDOM PROCESSES
Roberto
Vila
Departamento de Estatística, Universidade de Brasília, Brasília, Brasil
E-mail: rovig161@gmail.com
https://orcid.org/0000-0003-1073-0114
https://doi.org/10.21754/iecos.v24i2.2005
Recibido (Received): 09/12/2023 Aceptado (Accepted): 20/12/2023 Publicado (Published): 31/12/2023
RESUMEN
En este trabajo desenvolvemos extensivamente algunos de los resultados obtenidos en la referencia (Cioletti et al., 2017). Usamos la distancia de Wasserstein para obtener algunos teoremas del tipo limite central para procesos aleatorios unidimensionales que tienen dependencia asociada positiva.
Palabras claves: Distancia de Wasserstein; Proceso aleatorio, Asociado positivo.
ABSTRACT
In this paper we extensively develop some of the results obtained in reference (Cioletti et al., 2017). We use the Wasserstein distance to obtain some central limit type theorems for one-dimensional random processes having positive associated dependence.
Keywords: Wasserstein distance; Random process, Positive associate.
1. INTRODUCCIÓN
La distancia de Wasserstein 
también conocida como
Monge-Kantorovich-Rubinstein (Kantorovi
& Rubin
te
n, 1958; Jordan et al.,
1998),
distancia de Mallows (1972) o distancia de transporte optima en optimización (Ambrosio,
2003),
es responsable de medir la discrepancia entre dos medidas de probabilidades 
y
. Esta métrica ha sido
aplicada con éxito en una amplia variedad de campos, por ejemplo, Gray (2009),
Rachev y Rüschendorf
(1998), Sommerfeld y Munk (2018), Otto (2001) y Villani (2003, 2009).
Sobre los números reales, esta distancia cuantifica la discrepancia entre dos
funciones de distribución (acumulativas) 
y
. Si y
son las funciones de
distribución de dos variables aleatorias 
e
, respectivamente. El
Teorema de representación de Dorea y Ferreira (2012) nos permite
escribir, 
si 
donde
es el limite superior de
Frèchet. Además, puede ser demostrado que la representación 
donde 
es el límite inferior de
Frèchet, es válida en el caso que 
. Usando esas
representaciones y el conocido Teorema de Bickel y Freedman (1981),
(1)
el cual proporciona una estrecha relación con la
convergencia en distribución 
, en este trabajo haremos
uso de la distancia de Wasserstein (Vaserstein, 1969) para analizar el
comportamiento asintótico de procesos aleatorios unidimensionales que tienen
dependencia asociada positiva. Ejemplos de procesos aleatórios que exhiben este
tipo de comportamiento, por médio de 
, usualmente son
encontrados en la Mecánica Estadística, por ejemplo, en modelos ferromagnéticos
tipo Ising con espines discretos y contínuos, para mayores detalles, vea
referencia (Cioletti
et al., 2017).
2. LA DISTANCIA DE WASSERTEIN
En esta sección presentamos algunos conceptos de asociación positiva y de distancia de Wasserstein. En seguida, enunciamos algunos resultados preliminares que utilizaremos a lo largo de la exposición de este trabajo. Así mismo, cerramos esta sección con algunas definiciones adicionales.
2.1. ASOCIACIÓN POSITIVA.
Denote por 
al conjunto de los
números enteros. Consideraremos procesos aleatorios del siguiente tipo 
los cuales son definidos
sobre algún espacio de probabilidad 
y están asociados
positivamente de acuerdo a la siguiente definición.
Definición 1. Un proceso
aleatorio es asociado positiva si,
dadas dos funciones coordenadas no decrecientes 
y 
tenemos
(Gabriel, 2017)
siempre que la covarianza exista.
Decimos que una función 
es no decreciente si 
siempre que 
para todo 
Algunos ejemplos de procesos asociados positivamente son los siguientes:
Ejemplo 2. Cualquier conjunto de variables aleatorios independientes está asociado positivamente (Esary et al., 1967).
Ejemplo 3. Variables aleatorias con distribución Gaussiana multivariada y con covarianza positiva están asociadas positivamente (Pitt, 1982).
Ejemplo 4. Sean 
independiente e
idénticamente distribuidos y sea Y independiente de , entonces, {
} es asociado positivo (Barlow & Proschan, 1975).
Lema 5. Sea {
} un proceso aleatorios
asociado positiva; Para 
si 
son funciones
coordenadas no decrecientes, entonces {
}, también, es asociado
positivo (Oliveira,
2012).
Ahora, con el Lema 5 a nuestra disposición, es sencillo generar nuevas familias de variables aleatorias asociadas positivamente a partir de un conjunto de variables aleatorias con esta propiedad, al aplicar transformaciones monótonas.
Ejemplo 6. Si 
, son variables
aleatorios asociados positivas, entonces, la secuencia de sumas parciales 
esta asociada
positivamente. Esto es una consecuencia inmediata del Lema 5.
Ejemplo 7. Dadas las variables aleatorias 
, definan las
estadísticas ordenadas 
“el k-ésimo más pequeño
entre 
Estas estadísticas de
orden son transformaciones no decrecientes de , consecuentemente,
estas estadísticas de orden están asociadas positivamente, lo mismo se aplica a
Ejemplo 8. Dada una secuencia de variables aleatorias 
con 
fijo, defina 
, con 
fijo. Si los 
están asociadas, también
lo están los 
.
2.2. DISTANCIA DE WASSERSTEIN
En esta parte definimos el concepto de distancia de Wasserstein (Mallows, 1972; Newman, 1980) y establecemos una equivalencia con la definición de distancia Mallows que aparecen en las referencias (Bickel & Freedman, 1981; Dorea & Ferreira, 2012; Mallows, 1972) (ver Lema 10).
Sea (
) un espacio medible
correspondiente a un experimento aleatorio dado. Denotando por 
a la σ-álgebra de
los borelianos de 
, definimos la colecci´on
de todas las medidas de probabilidad sobre por 
.
Supongamos que estamos encargados del “transporte de
mercancías” entre productores e consumidores, cuyas distribuciones espaciales
son modeladas por las medidas de probabilidad y
. Si los productores y
consumidores estan localizados a una distancia mayor, mas difícil será nuestro
trabajo. Luego, nos gustaría resumir el “grado de dificultad” con apenas una
cantidad. Para ello, es natural considerar el “costo óptimo de transporte”
entre las medidas y como
(Gabriel, 2017)
donde 
denota el costo de
transporte de una unidad de masa de 
para 
y el conjunto
(2)
(Gabriel, 2017)
está constituido por todos los acoplamentos 
de
, conocidos como planos
de transporte. Aquí, 
, para cada borelianos A
y B en 
, son la proyecciones
sobre la medida . En terminos simples, 
es el conjunto de todas
las medidas de probabilidad 
con marginales y
, respectivamente. En
general C no es una distancia. En el caso que c sea una
distancia, entonces C es una distancia (métrica), también.
Definición 9 (Distancia de
Wasserstein). Sea (
) un espacio m´etrico,
con métrica dada por d : 
→ [0, ∞). La
distancia de Wasserstein de orden r > 0 entre dos medidas de probabilidad 
se define mediante la
siguiente fórmula (Mallows, 1972; Villani, 2009):
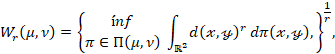
donde es el conjunto
definido en (2).
Algunos casos particulares de la distancia de Wasserstein son conocidos, por ejemplo (Gabriel, 2017):
·
esa expresión es llamada
“fórmula de dualidad para la distancia de Kantorovich-Rubinstein”, para mayores
detalles, ver Villani (2003). Aquí el supremo es tomado sobre todas las
funciones Lipschitzianas (limitadas) ψ que están dentro de la bola unitaria,
según la norma 
, donde 
y 
.
·
donde 
y 
son medidas de delta de
Dirac concentradas en los puntos fijos e , respectivamente.
·
Si
es una métrica discreta,
es decir 
entonces 
(ver [21]), donde 
denota la distancia de
variación total entre y 
El siguiente resultado nos ofrece una caracterización
de la distancia de Wasserstein en el caso que está equipado con la
métrica euclidiana. La prueba de este resultado puede ser encontrado en el
Apéndice A. En algunas referencias, vea por ejemplo (Bickel & Freedman,
1981; Dorea & Ferreira, 2012; Mallows, 1972), esta medida es conocido como
distancia Malllows.
Lema 10. En la Definición 9,
considere 
y 
dos
funciones de distribución (acumulativa). Entonces, la distancia de Wasserstein
de orden 
entre F y G es dada por
donde el infimo es tomado sobre todos los pares de variables aleatorios (X,Y) cuyas distribuciones marginales son F y G, respectivamente.
Tenga en cuenta que, estrictamente hablando, , como definido
anteriormente, no es una distancia sobre el espacio de las funciones de
distribución, ya que esta definición admite la posibilidad 
. Pero esto no crea
ningún inconveniente, para que esta definición tenga sentido las distribuciones
y deben
tener un momento (absoluto) de orden r finito. Formalmente, definimos el
espacio de distribuciones que tienen esta propiedad por
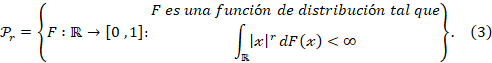
Este espacio fue introducido por Bickel y Freedman (1981)
para mostrar que, para 
la función 
en el Lema 10 es una
métrica.
Observación 11. De aquí en adelante,
en este trabajo, usaremos la definición de la distanción de Wassertein
providenciada por el Lema 10. Esto es, consideraremos la Definición 9
consideramos la métrica euclidiana 
2.3. RESULTADOS Y DEFINICIÓN PRELIMINARES
A continuación recopilamos algunos resultados, propiedades y definiciones necesarias para las pruebas de este trabajo.
Lema 12 (Newman & Wright,
1981). Sea 
un proceso aleatorio
asociado positivo; Si todos los 
poseen un segundo
momento finitom entonces las funciones características 
y
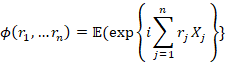
satisfacen
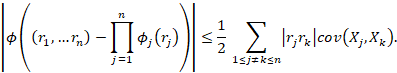
El lema 12 nos informa que, para procesos aleatorios asociados positivos cuyas combinaciones lineales de las covarianzas poseen un determinado decaimiento a medida que n cresce, el proceso puede ser considerado asintoticamente independiente.
Asuma que 
y 
tienen distribuciones 
Y 
,
respectivamente, donde 
El siguiente resultado (Teorema 13) facilita la
evaluación de 
pues en este caso la
distancia de Wassersteins con es
alcanzado por el r-ésimo momento de 
con respecto a la
distribución H.
Teorema 13 (Dorea & Ferreira,
2012). Para 
la distancia de
Wasserstein del Lema 10 puede ser escrita como
donde U es uniformemente distribuida sobre el intervalo (0,1) y
(Gabriel, 2017)
denota la inversa generalizada.
La representación de la distancia de Wasserstein del
Teorema 13 no es valida para 
incluso cuando el
momento de orden r es finito, como se
muestra en el siguiente ejemplo:
Ejemplo 14. Sean 
dos variables aleatorias
discretas con respectivas funciones de probabilidades dadas por
Denota por y
a las funciones de
distribución de e ,
respectivamente.
Supongamos que 
y que 
, es decir, las funciones
de distribución de y 
respectivamente, son
definidas como,
Vea que las distribuciones de probabilidades de 
y 
son
explícitamente dadas por (Tabla 1):
Tabla 1
Distribuciones de probabilidades de y 
Observe que
Una vez que la función 
es positiva, 
tenemos que 
Por lo tanto, para cualquier no
es posible obtener una representación de la distancia de Wasserstein como la
del Teorema 13.
Observación 15. Una generalización del Ejemplo 14 puede ser encontrada en la referencia (Dorea & Ferreira, 2012).
Ahora, asuma que, y tienen distribuciones 
respectivamente, donde,
El próximo resultado (Teorema 16) facilita la
evaluación de pues en este caso con tienen
una expresión cerrada en función de r-ésimo momento de 
con
respecto K.
Teorema 16. Para la
distancia de Wassertein del Lema 10 puede ser escrita como
donde U es uniformemente distribuida sobre el intervalo (0,1).
Ejemplo 17. Sean 
y
las variables aleatorias
consideradas en el Ejemplo 14. Una vez que, para cualquier
concluimos que, para
no es posible obtener
una representación de la distancia de Wasserstein como la del Teorema 16.
Definición 18 (Convergencia). Sean 
y funciones
de distribución. Diremos que 
converge em dist
ncia de Wasserstein a ,
si
El siguiente lema básicamente nos brinda una conexión
directa entre la convergencia en distancia de Wasserstein 
y la convergencia en
distribución. Para ello es necesario recordar la definición del conjunto 
en (3).
Teorema 19 (Bickel & Freedman,
1981). Si 
entonces si y solamente si,
·
· 
En otras palabras, el Teorema de Bickel y Freedman arma que convergencia en distancia de Wasserstein es un concepto mas fuerte que convergencia en distribución. Para variaciones y extensiones de este resultado, consulte las referencias (Dorea & Ferreira, 2012; Shorack & Wellner, 2009).
Definición
20. Un proceso
aleatorio 
es
estacionario (fuerte) si para todo 
y 
Donde 
denota igualdad en
distribución.
La demostración del siguiente resultado puede ser encontrado en detalle en el Apéndice B de este trabajo.
Proposición 21. Sea
un
proceso aleatorio estacionario. Para 
si
son
funciones medibles, entonces 
también
es estacionario.
Teorema
22 (Newman, 1980).
Sea un
proceso aleatorio estacionario y asociado positivo. Supongamos que la varianza
es finita y estrictamente positiva, 
,
y que
Entonces,
Proposición
23. Convergencia
de una serie monótona (Yeh, 2006). Si para todos los números naturales 
y 
, 
es
un número real no negativo y 
entonces
3. TEOREMAS DEL LÍMITE CENTRAL
Sea un
proceso aleatorio estacionario en el sentido de la Definición 20. Para procesos
estocásticos es natural, cuando lidamos con teoremas límites, considerar
bloques de 
variables
aleatorias consecutivas,
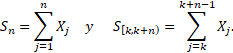
Claramente,
bajo el supuesto de estacionariedad tenemos 
,
para todo 
,
esto es, 
y
tienen
la misma función de distribución. Para verificar esto basta considerar la
función (medible) 
en
la Proposición 21.
Cabe
mencionar que la asociatividad positiva y la estacionariedad aseguran que, 
en
(6) pueda ser escrita como
y que este
a bien definida. En Mecánica Estadística 
es
conocida como la susceptiblidad correspondiente al proceso aleatorio 
Defina la variable aleatoria
con su respectiva función de distribución (acumulativa), dada por
lo cual por simplicidad denotamos como 
El primer resultado (Teorema 24), extraído de la referencia (Cioletti et al., 2017), se desprende del Teorema del límite central (TLC) de Newman (Teorema 22).
Teorema 24 (Cioletti et al., 2017). Sea
un
proceso estacionario y asociado positivo. Supongamos que la varianza es finita
y estrictamente positiva ,
y que
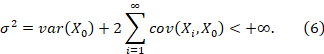
Para 
, tenemos
donde 
denota la función de
distribución de la distribución normal estándar 
la cual, para
simplificar, usualmente escribiremos como 
.
Demostración. Sabemos que, por estacionariedad, 
Consecuentemente, ambas
variables tienen los mismos momentos de orden finito, y por tanto, la misma
varianza. Luego
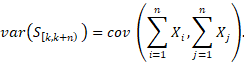
Usando la bilinealidad y la simetría de la covarianza, la expresión anterior puede ser escrita como
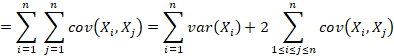
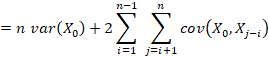
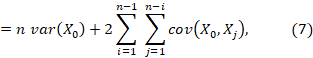
donde en la cuarta igualdad, nuevamente, usamos la
estacionalidad del proceso. Note que los elementos de la suma 
pueden ser reordenados
de la siguiente forma:
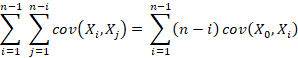
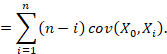
Usando este reordenamiento, (7) es
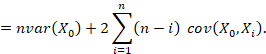
Luego, tenemos
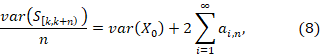
donde 
es definida por
Vea que, por asociatividad, 
y que 
. Luego, usando la
Proposición 23 sobre convergencia de series monótonas, sigue que
Sustituyendo el límite anterior en (8), de (6) se deduce que
De este modo,
donde 
. Como 
es convergente, es acotada, y claramente
. Dado que se cumple la
convergencia en distribución (4), Teorema de Newman (1980), concluimos del
Teorema 19 de Bickel y Freedman que 
A continuación, para extender la convergencia para 
hacemos
uso del Teorema de representación 13 de Dorea y Ferreira. Existe una variable
aleatoria 
tal que la distribución
conjunta de 
está dada por 
y
Usando el Lema 10 y la Desigualdad de Lyapunov
tenemos, para 
donde hemos usado la convergencia en (10).
Para derivar la convergencia de orden superior para , se requerirán
condiciones de momento adicionales en 
. Para 
, sea 
el coeficiente de
Cox-Grimmet, definido por
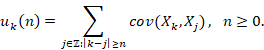
Tenga en cuenta que, según el Lema 12, el proceso
aleatorio 
también es estacionario
y está asociado positivamente. Esto nos permite plantear una desigualdad de
momentos de Birkel (1988) adaptada a nuestras necesidades.
Lema 25 (Cioletti et al., 2017).
Sean 
y 
un proceso estacionario
y asociado positivo. Supongamos que 
y que para algunas
constantes 
y
tenemos 
Entonces existe una
constante 
tal que
Demostración. La prueba se desprende inmediatamente del Corolario 2.21 en Oliveira (2012).
Note que, según el Teorema 24, tenemos satisfechas las
condiciones del Lema 25 para 
. De hecho, por (6)
tenemos 
y (11) sigue de (9).
El siguiente teorema, extraído de la referencia (Cioletti
et al., 2017), nos brinda una extensión de la convergencia en distancia de
Wasserstein para ordenar 
mayores que 2.
Teorema 26 (Cioletti et al., 2017).
Sean y 
un proceso estacionario
y asociado positivo. Supongamos que y que para algunas
constantes y
se satisface 
. Entonces, si 
, dada por (6), es
tal que 
tenemos
y 
donde 
y 
se define mediante (5);
y Z
Demostración.
Tenga en cuenta que para 
el Teorema de Newman
(Teorema 22) implica 
Luego, para completar la
prueba del teorema, necesitamos demostrar que
y 
En este caso la convergencia 
sigue inmediatamente por
aplicar el Teorema de Bickel y Freedman (Teorema 19).
Si demostramos que la secuencia 
es uniformemente
integrable, entonces, por usar resultados estándar en la literatura, tendríamos
la validez de la convergencia 
en (12).
Para demostrar que es uniformemente
integrable, basta probar la siguiente integración uniforme: para algún 
lo cual implicaría que 
De hecho, usando la
Desigualdad de Lyapunov tenemos
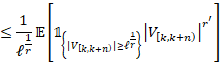
Bajo la condición 
,
al tomar 
y luego 
en la desigualdad
anterior, la integrabilidade uniforme de 
sigue inmediatamente.
Sea 
Se deduce que existen 
tales que 
Simplemente tome 
Además, 
pues 
es
creciente. Del Lema 25 tenemos, para 
Resulta que,
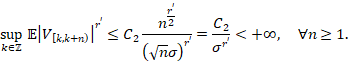
Esto concluye la prueba del teorema.
Como aplicación de los Teoremas 24, 26 y el Lema 28 (vea Apéndice C), tenemos el siguiente resultado de convergencia:
Corolário 27. Si el proceso
aletorio satisface las hipótesis
del Teorema 24 (o Teorema 26), entonces
donde 
es la distancia de
Kolmogorov enter F y G.
AGRADECIMIENTO
RV agradece la invitación de los organizadores del evento I CONGRESO INTERNACIONAL DE INVESTIGACIÓN De Ingeniería Económica, Estadística y Ciencias Sociales.
APÉNDICE A. DEMOSTRACIÓN DEL LEMA 10
La prueba de este resultado requiere el uso del Teorema de cambio de variables.
Nuestro objetivo principal es demostrar que
y que
Primero, demostraremos la desigualdad en (13). Para
ello, considere un vector aleatorio 
, definido sobre algún
espacio de probabilidad cuyas distribuciones
marginales de e son
dadas por y 
respectivamente.
Si 
denota la distribución
conjunta de Z, entonces las distribuciones marginales de son dadas por:
Considere la función Borel medible 
definida por 
. Usando la definición de
esperanza y aplicando el Teorema de cambio de variables, obtenemos
Afirmamos que 
. De hecho, esto es
inmediato, pues
donde en la ´ultima igualdad usamos (15). De forma similar, tenemos
lo cual prueba la afirmación.
Los argumentos anteriores muestran que, para cada
vector aleatorio cuyas distribuciones
marginales están dadas por y ,
existe una medida de probabilidad 
, tal que
Como consecuencia de esta igualdad y de la definición del ínfimo, obtenemos
Esto es, la desigualdad en (13) es satisfecha.
Ahora demostraremos la desigualdad recíproca en (14).
De hecho, dado 
considere el espacio de
probabilidad 
y las variables
aleatorias (proyecciones) 
y
definidas por 
y 
, respectivamente. Desde
que , las distribuciones
marginales del vector (
) son y
, respectivamente. Usando
la definición de las variables y, tenemos
Así, para cada se construyó un vector
aleatorio () que tiene como
distribuciones marginales a y ,
respectivamente, de modo que se cumple la igualdad anterior. Por lo tanto,
hemos demostrado que
Por lo tanto,
Esto es, la desigualdad en (14) es válida.
De (13) y (14) la prueba del lema sigue inmediatamente.
APÉNDICE B. DEMOSTRACIÓN DE LA PROPOSICIÓN 21
Debemos verificar que, 
De hecho, por cada 
tenemos
donde 
es la imagen de 
y 
es un boreliano de 
Una vez qué es estacionario, vea
que,
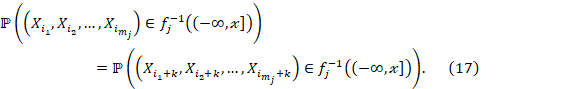
De (16) y (17) obtenemos, 
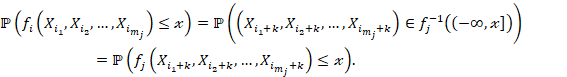
En otras palabras, 
, las variables
aleatorias 
y
son iguales en
distribución. Esto concluye la demostración.
APÉNDICE C. UN RESULTADO ADICIONAL
Lema 28. Sean e
dos variables aleatorias
tal que es absolutamente
continua con densidad 
tal que 
,
y para alguna constante 
. Entonces,
donde 
es la distancia de
Kolmogorov entre las distribuciones 
y 
Demostración. Dado 
y
fijo, definimos
Para cada 
note que
lo cual implica que 
y 
son funciones Lipschitz
con constante Lipschiptz 
.
Dado que
Obtenemos
donde hemos usado el hecho de que es Lipschitz. Por la
desigualdad anterior y de la definición de la distancia de Wasserstein se
deduce que
De forma análoga, usando que es Lipschitz,
encontramos que
Por lo tanto,
Una vez que la función 
tiene un valor máximo 2
en 
la demostración del
corolário sigue rápidamente.
REFERENCIAS
Ambrosio, L. (2003). Lecture Notes on Optimal Transport Problems. In: Ambrosio, L., Deckelnick, K., Dziuk, G., Mimura, M., Solonnikov, V. A., Soner, H. M., & Ambrosio, L. (Eds.), Mathematical Aspects of Evolving Interfaces (pp. 1-52). Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-540-39189-0_1
Barlow, R. E., & Proschan, F. (1975). Statistical theory of reliability and life testing: probability models. Holt, Rinehart and Winston.
https://apps.dtic.mil/sti/citations/ADA006399
Bickel, P. J., & Freedman, D. A. (1981). Some asymptotic theory for the bootstrap. The annals of statistics, 9(6), 1196-1217. https://doi.org/10.1214/aos/1176345637
Birkel, T. (1988). Moment bounds for associated sequences. The annals of Probability, 16(3), 1184-1193. https://www.jstor.org/stable/2244116
Cioletti, L., Dorea, C. C. Y., & Vila, R. (2017). Limit Theorems in Mallows Distance for Processes with Gibssian Dependence. arXiv.
https://doi.org/10.48550/arXiv.1701.03747
Dorea, C. C., & Ferreira, D. B. (2012). Conditions for equivalence between Mallows distance and convergence to stable laws. Acta Mathematica Hungarica, 134(1-2), 1-11. https://doi.org/10.1007/s10474-011-0101-7
Esary, J. D., Proschan, F., & Walkup, D. W. (1967). Association of random variables, with applications. The Annals of Mathematical Statistics, 38(5), 1466-1474.
https://doi.org/10.1214/aoms/1177698701
Gabriel, R. V. (2017). Representações gráficas para sistemas de spins com presença de campo externo: algumas relações em teoria de probabilidades [Tese para obtenção do grau de Doutor em Matemática]. Universidade de Brasília. Instituto de Ciências Exatas. Departamento de Matemática. http://icts.unb.br/jspui/handle/10482/22471
Gray, R. M. (2009). Probability, random processes, and ergodic properties. Springer. https://doi.org/10.1007/978-1-4419-1090-5
Jordan, R., Kinderlehrer, D., & Otto, F. (1998). The variational formulation of the Fokker--Planck equation. SIAM journal on mathematical analysis, 29(1), 1-17.
https://doi.org/10.1137/S0036141096303359
Kantorovi
, L. V., Rubin
te
n, G. 
. (1958). On a space of completely additive functions.
Vestnik Leningrad University, 13, 52-59.
Mallows, C. L. (1972). A note on asymptotic joint normality. The Annals of Mathematical Statistics, 43(2), 508-515. https://www.jstor.org/stable/2239988
Newman, C. M. (1980). Normal fluctuations and the FKG inequalities. Communications in Mathematical Physics, 74(2), 119-128. https://doi.org/10.1007/BF01197754
Newman, C. M., & Wright, A. L. (1981). An invariance principle for certain dependent sequences. The Annals of Probability, 9(4), 671-675.
https://doi.org/10.1214/aop/1176994374
Oliveira, P. E. (2012). Asymptotics for associated random variables. Springer Science & Business Media.
Otto, F. (2001). The geometry of dissipative evolution equations: the porous medium equation. Communications in Partial Differential Equations, 26(1-2), 101-174.
https://doi.org/10.1081/PDE-100002243
Pitt, L. D. (1982). Positively correlated normal variables are associated. The Annals of Probability, 10(2), 496-499. https://www.jstor.org/stable/2243445
Rachev, S. T., & Rüschendorf, L. (1998). Mass Transportation Problems: Volume I: Theory. Springer Science & Business Media.
Shorack, G. R., & Wellner, J. A. (2009). Empirical processes with applications to statistics. Society for Industrial and Applied Mathematics.
https://epubs.siam.org/doi/pdf/10.1137/1.9780898719017.bm
Sommerfeld, M., & Munk, A. (2018). Inference for empirical Wasserstein distances on finite spaces. Journal of the Royal Statistical Society Series B: Statistical Methodology, 80(1), 219-238. https://doi.org/10.1111/rssb.12236
Vaserstein, L. N. (1969). Markov processes over denumerable products of spaces, describing large systems of automata. Problemy Peredachi Informatsii, 5(3), 64-72. https://www.mathnet.ru/eng/ppi1811
Villani, C. (2003). Topics in optimal transportation. OR/MS Today, 30(3), 66-67. https://link.gale.com/apps/doc/A104669453/AONE?u=anon~6226aa1c&sid=googleScholar&xid=2585334e
Villani, C. (2009). Optimal transport: old and new. Springer.
https://doi.org/10.1007/978-3-540-71050-9
Yeh, J. (2006). Real Analysis: Theory of Measure and Integration. World Scientific.